Spring Constant Units EXPLAINED! (You Won't Believe #3!)

Understanding units for spring constant is crucial for anyone working with systems involving elasticity. Hooke's Law provides the fundamental relationship between force and displacement in a spring, making the spring constant, typically represented by k, a vital parameter. The SI system, the internationally recognized standard of units, dictates that force is measured in Newtons (N) and displacement in meters (m). Thus, units for spring constant are expressed as Newtons per meter (N/m). However, variations such as pounds per inch (lb/in) or dynes per centimeter (dyn/cm) exist, particularly within engineering applications, requiring conversions for accurate calculations.

Image taken from the YouTube channel Physics with Professor Matt Anderson , from the video titled How to determine the spring constant .

Ever wondered what gives a pogo stick its bounce? Or how a simple spring in a ballpoint pen can withstand thousands of clicks? The answer, in part, lies within a deceptively simple concept: the spring constant.

The Spring Constant: More Than Meets the Eye

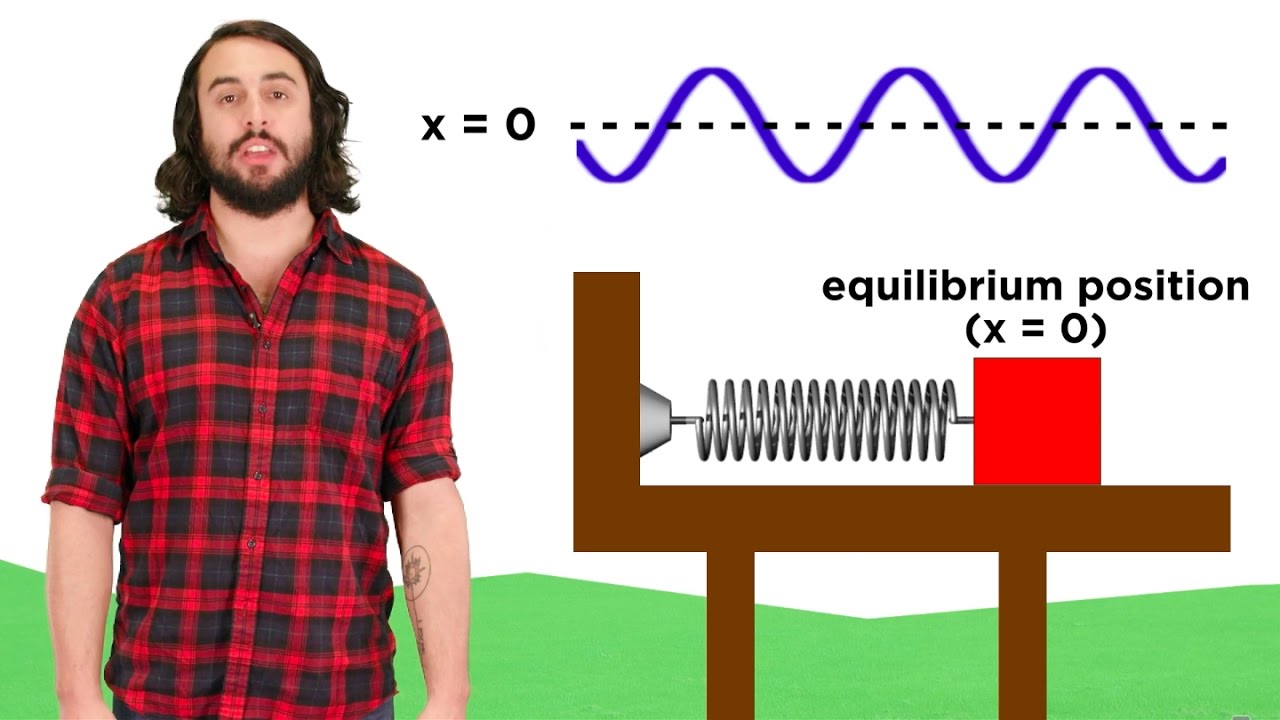
The spring constant, often denoted as 'k', is a fundamental property that quantifies the stiffness of a spring. It dictates the amount of force required to stretch or compress a spring by a certain distance.

Understanding the spring constant is crucial in various fields, from mechanical engineering to materials science. It allows us to predict and control the behavior of springs in countless applications.

The Unsung Heroes: Units of Measurement

But here’s where things get interesting: simply knowing the spring constant isn’t enough. The units used to express it are equally, if not more, important. Using the correct units ensures accurate calculations and prevents costly errors.

Imagine designing a suspension system for a car using the wrong units for the spring constant! The consequences could range from an uncomfortable ride to a complete system failure.

A Teaser of Surprises

What if I told you that the spring constant isn’t just an inherent property of the spring itself? What if factors like the spring's material, its coil diameter, and even the thickness of the wire play a significant role in determining its value?

This may sound surprising, but it's true! Understanding these hidden influences is the key to truly unlocking the secrets of the spring constant. This unexpected twist highlights the importance of delving deeper into the fascinating world of spring mechanics.

Ever wondered what gives a pogo stick its bounce? Or how a simple spring in a ballpoint pen can withstand thousands of clicks? The answer, in part, lies within a deceptively simple concept: the spring constant.

This may sound surprising, but it's true! Understanding these hidden influences is the key to truly unlocking the secrets of the spring constant. This naturally leads us to a more rigorous definition of what the spring constant actually is.

Defining the Spring Constant: A Measure of Stiffness

At its core, the spring constant (k) is a numerical representation of a spring's inherent stiffness.

Think of it as a measure of how much force is needed to stretch or compress a spring by a specific distance.

A high spring constant indicates a stiff spring, requiring a significant amount of force to produce even a small displacement.

Conversely, a low spring constant signifies a more flexible spring, easily stretched or compressed with minimal force.

Resisting Deformation: The Spring's Natural Inclination

The spring constant also reveals a spring's ability to resist deformation.

When a force is applied to a spring, the spring exerts an equal and opposite force to return to its original, undeformed state.

The spring constant quantifies this resistance. The higher the value of k, the greater the force the spring exerts to counteract the applied force and maintain its original form.

Spring Constant in Action: Real-World Examples

The spring constant isn't just an abstract concept; it's a critical parameter in numerous real-world applications:

Car Suspension Systems: Car suspensions rely on springs with carefully chosen spring constants to absorb shocks and vibrations from the road, providing a comfortable ride. A stiffer suspension (higher k) will result in a firmer ride.

Ballpoint Pens: The small spring inside a ballpoint pen uses a specific k value to ensure the pen retracts smoothly and reliably after each click.

Weighing Scales: Many weighing scales utilize springs to measure weight. The displacement of the spring, governed by its k value, is directly proportional to the applied force (weight).

Medical Devices: From surgical instruments to ventilators, springs with precise k values are essential for accurate and controlled movements in various medical devices.

These examples show how critical understanding k is to the functionality of so many aspects of modern life.

The spring constant isn't just some arbitrary number assigned to a spring. It's deeply intertwined with the fundamental physics that govern how springs behave. It’s time to explore the bedrock upon which spring behavior is understood: Hooke's Law.

Hooke's Law: The Foundation of Spring Behavior

Hooke's Law is the cornerstone for understanding how springs work. It elegantly describes the linear relationship between the force applied to a spring and the resulting displacement. But what does this mean in practical terms?

Decoding the Equation: F = -kx

The mathematical representation of Hooke's Law is deceptively simple: F = -kx. This compact equation holds a wealth of information. Each term is crucial to understanding the principle.

• F represents the force applied to the spring.
• k, as we've discussed, is the spring constant.
• x (or sometimes Δx) signifies the displacement of the spring from its equilibrium position. It means the amount the spring is stretched or compressed.

The negative sign is equally important. It indicates that the force exerted by the spring is in the opposite direction to the applied force. The spring is resisting the change.

Force and Displacement: A Direct Relationship

Hooke's Law tells us that the force required to stretch or compress a spring is directly proportional to the displacement.

Double the displacement, and you double the force needed. This relationship is linear, meaning it forms a straight line when graphed.

This linearity is a key characteristic of springs operating within their elastic limit.

The Role of Elasticity

Elasticity is the ability of a material to return to its original shape after being deformed. Hooke's Law applies specifically when a spring is deformed elastically.

If you stretch a spring beyond its elastic limit, it will experience plastic deformation. That deformation means it will not return to its original shape, and Hooke's Law no longer holds true.

The spring's behavior becomes more complex and less predictable. Thus, elasticity ensures that the spring force is directly proportional to the displacement, as described by Hooke's Law.

Hooke's Law elegantly lays out the relationship between force, displacement, and the spring constant, but the true power of this relationship is fully realized when we understand the units involved. Now, let’s pull back the curtain on the standard unit of the spring constant and explore why it is what it is.

SI Units Demystified: Newton per Meter (N/m) Explained

The spring constant, that crucial measure of a spring's stiffness, is expressed in the International System of Units (SI) using Newton per Meter (N/m). This isn't an arbitrary choice; it directly reflects the fundamental relationship defined by Hooke's Law. Let's unpack what this means and why it's so important.

Understanding Newton per Meter

The unit N/m directly stems from Hooke's Law (F = -kx).

Remember, 'F' represents force (measured in Newtons) and 'x' represents displacement (measured in meters).

Therefore, to isolate 'k' (the spring constant), we rearrange the equation to k = F/x.

This rearrangement makes it clear: the spring constant is force divided by displacement.

The SI unit for force is the Newton (N), and the SI unit for displacement is the meter (m).

Combining these, we get N/m.

This means the spring constant tells us how many Newtons of force are required to stretch or compress the spring by one meter.

Force Required Per Unit of Displacement

The beauty of N/m lies in its direct interpretability. A spring with a spring constant of 100 N/m, for instance, requires 100 Newtons of force to stretch it one meter.

Similarly, it requires the same amount of force to compress it by one meter from its resting position.

This direct relationship makes comparing the stiffness of different springs incredibly straightforward.

A higher N/m value indicates a stiffer spring, as it takes more force to achieve the same amount of displacement.

Conversely, a lower N/m value indicates a more compliant spring.

Practical Examples of Spring Stiffness

Let's consider some tangible examples to solidify our understanding:

• A Stiff Car Suspension Spring: A heavy-duty spring used in a car's suspension might have a spring constant of 50,000 N/m. This high value reflects the large force needed to compress the spring and absorb bumps in the road.

• A Typical Ballpoint Pen Spring: The small spring inside a ballpoint pen, on the other hand, might have a spring constant of only 5 N/m. The small value reflects how little force is needed to extend or compress the spring.

• A Soft Toy Spring: Imagine a spring used in a soft toy. It should be easy to push. Therefore, the spring constant could be as low as 1 N/m.

By understanding the units of the spring constant, we gain a powerful tool for predicting and controlling the behavior of springs in a wide range of applications. The N/m unit provides a clear and intuitive measure of spring stiffness.

Hooke's Law elegantly lays out the relationship between force, displacement, and the spring constant, but the true power of this relationship is fully realized when we understand the units involved. Now, let’s pull back the curtain on the standard unit of the spring constant and explore why it is what it is.

Unit Conversions: Mastering the Metric System and Beyond

While the SI system reigns supreme in scientific circles, clinging to a single system without understanding conversions can lead to costly mistakes. The world isn't solely measured in meters, and sometimes, centimeters become unavoidable. Here's why mastering unit conversions is crucial for anyone working with spring constants, and how to navigate the potential pitfalls.

The Ubiquitous Centimeter: Bridging the Gap to Meters

The centimeter (cm), a seemingly innocuous unit, often appears in practical measurements and experimental setups. Since the SI unit for length is the meter, using centimeters requires immediate conversion to meters before any calculations involving Hooke's Law or spring constants.

Failing to convert introduces a scaling error, directly impacting the accuracy of your results. Remember that 1 meter is equal to 100 centimeters.

Therefore, a displacement of 25 cm must be expressed as 0.25 m for use in Hooke's Law (F = -kx) when the spring constant is in N/m.

Exploring the CGS System: Dynes and Centimeters

Before the widespread adoption of the SI system, the Centimeter-Gram-Second (CGS) system was a common standard. In CGS, force is measured in dynes and displacement in centimeters. Consequently, the spring constant in the CGS system is expressed as dyne per centimeter (dyn/cm).

The dyne isn't just an archaic unit; it represents a fundamental unit of force in a different measurement framework.

Understanding how to convert between N/m (SI) and dyn/cm (CGS) is essential for interpreting older research or working with equipment calibrated using CGS units.

The Critical Importance of Unit Consistency

Imagine calculating the force exerted by a spring using a spring constant in N/m and a displacement value in centimeters – the result would be completely nonsensical. This highlights the most vital principle: unit consistency is paramount.

Before performing any calculation, meticulously ensure that all quantities are expressed in a consistent set of units.

This might involve converting centimeters to meters, grams to kilograms, or even more complex conversions depending on the context of the problem.

Failing to maintain unit consistency is akin to adding apples and oranges; the resulting number is meaningless.

Practical Conversion Examples: Bridging the Divide

Let's explore some practical conversion examples to solidify the concept:

Converting N/m to dyn/cm

Given a spring constant of 50 N/m, what is its equivalent in dyn/cm?

• Recall: 1 N = 10⁵ dynes and 1 m = 100 cm
• Conversion: 50 N/m = 50 (10⁵ dynes) / (100 cm) = 5000 dyn/cm

Converting dyn/cm to N/m

Given a spring constant of 2000 dyn/cm, what is its equivalent in N/m?

• Recall: 1 dyne = 10^-5 N and 1 cm = 0.01 m
• Conversion: 2000 dyn/cm = 2000 (10^-5 N) / (0.01 m) = 2 N/m

These examples illustrate the direct relationship between the SI and CGS units for the spring constant. Master these conversions, and you'll minimize errors and ensure accurate calculations in any context.

The world isn't solely measured in meters, and sometimes, centimeters become unavoidable. Here's why mastering unit conversions is crucial for anyone working with spring constants, and how to navigate the potential pitfalls. Now, let's shift our focus inward, moving beyond the surface understanding of the spring constant as an inherent characteristic of a spring. Prepare to uncover the surprisingly complex interplay of factors that truly dictate a spring's stiffness.

The Surprise Factor: Unmasking the Spring Constant's True Nature

Many assume that the spring constant is an immutable property, intrinsic to each individual spring. This assumption, however, drastically oversimplifies reality. The spring constant is not solely determined by the spring itself. Instead, it's a delicate balance of several interwoven factors, a surprising fact that has profound implications for accurate design and engineering. Let's delve into what these factors are and how they collectively define a spring's behavior.

Material Matters: The Foundation of Elasticity

The very material from which a spring is crafted plays a pivotal role in determining its spring constant. Different materials possess inherent elastic properties, meaning they respond differently to applied forces. Steel, for example, is a common choice for springs due to its high elasticity and ability to return to its original shape after deformation.

However, even within steel, variations exist. The specific alloy used, its heat treatment, and its grain structure all influence the material's elasticity and, consequently, the spring constant.

Geometric Influences: Shaping Stiffness

Beyond the material itself, the geometry of the spring exerts a significant influence on its stiffness.

Coil Diameter: A Wider or Narrower Path?

The coil diameter is a key geometric factor. A spring with a smaller coil diameter will generally be stiffer (higher spring constant) than one with a larger diameter, assuming all other factors are equal.

This is because a smaller diameter translates to a shorter lever arm for the force to act upon, requiring a greater force to achieve the same displacement.

Wire Thickness: Strength in Numbers

The thickness of the wire used to form the spring is another critical determinant. A thicker wire provides greater resistance to bending, resulting in a higher spring constant.

Intuitively, this makes sense – a thicker wire is simply stronger and more difficult to deform.

Number of Coils: Sharing the Load

The number of active coils in a spring also impacts its spring constant. More coils generally lead to a lower spring constant, as the applied force is distributed over a greater length of the spring.

Imagine stretching a long Slinky versus a short section of the same Slinky; the shorter section is clearly more resistant to stretching.

Elasticity Revisited: A Collective Property

All these factors – material properties, coil diameter, wire thickness, and the number of coils – collectively determine the overall elasticity of the spring. Elasticity, in this context, describes the spring's ability to deform under stress and return to its original shape when the stress is removed. Understanding how these factors interact is crucial for designing springs with precise and predictable performance. By carefully selecting the material and tailoring the geometry, engineers can fine-tune the spring constant to meet the specific requirements of a given application.

The world isn't solely measured in meters, and sometimes, centimeters become unavoidable. Here's why mastering unit conversions is crucial for anyone working with spring constants, and how to navigate the potential pitfalls. Now, let's shift our focus inward, moving beyond the surface understanding of the spring constant as an inherent characteristic of a spring. Prepare to uncover the surprisingly complex interplay of factors that truly dictate a spring's stiffness.

Real-World Applications: Spring Constant Units in Action

The theoretical understanding of the spring constant is important, but its true significance is revealed when applied to real-world scenarios. From ensuring a smooth ride in your car to the precision of medical instruments, the spring constant, and, crucially, its units, play a vital role.

Let's explore a few key areas where a solid grasp of spring constant units is not just helpful but essential for success and accuracy.

Suspension Systems: The Ride Quality Connection

Think about the suspension system in a vehicle. Springs are a core component, absorbing shocks and vibrations from the road. The spring constant of these springs directly affects the ride quality.

A spring with an inappropriately high spring constant will create a very bumpy and rigid experience, which the vast majority of people would find uncomfortable.

A spring with too low a spring constant will make the car feel as though it's floating, and in extreme circumstances could bottom out or struggle to return to its starting state when driving over successive bumps.

But what happens if the engineers use the wrong units during design calculations?

Imagine calculating the spring constant needed for a specific vehicle weight and desired suspension travel, but using centimeters instead of meters, and forgetting to correct for it.

The resulting spring could be significantly stiffer or softer than intended, leading to a harsh or unstable ride. Correct units are therefore critical to ensure the vehicle performs as intended.

Weighing Scales: Force Measurement Precision

Weighing scales, from the simple kitchen scale to sophisticated industrial models, often rely on springs to measure force.

When you place an object on the scale, it compresses a spring. The amount of compression is proportional to the object's weight (force), according to Hooke's Law.

The scale then converts this displacement into a weight reading. However, the accuracy of this reading depends directly on the accurate calibration of the spring and a correct understanding of the spring constant's units.

If the spring constant is expressed in dynes per centimeter, and the calculation mistakenly treats it as Newtons per meter, the weight displayed will be drastically incorrect.

Medical Devices: Engineering for Delicate Applications

In the world of medical devices, precision is paramount. Many devices, from drug delivery systems to surgical instruments, incorporate springs. The correct spring constant, and its units, are crucial for proper function.

Consider a device designed to deliver a specific dose of medication. The spring's compression might control the amount of fluid released.

An error in the spring constant calculation, even a small one, could lead to an incorrect dosage, potentially with serious consequences for the patient.

Therefore, engineers in the medical field must have a meticulous understanding of spring constants and their units to ensure patient safety and treatment efficacy.

These are just a few examples of the far-reaching impact of understanding spring constant units. Whether it's ensuring a comfortable ride, measuring weight accurately, or delivering precise medical treatments, the correct application of spring constant knowledge is fundamental to engineering and scientific success.

Video: Spring Constant Units EXPLAINED! (You Won't Believe #3!)

Play Video