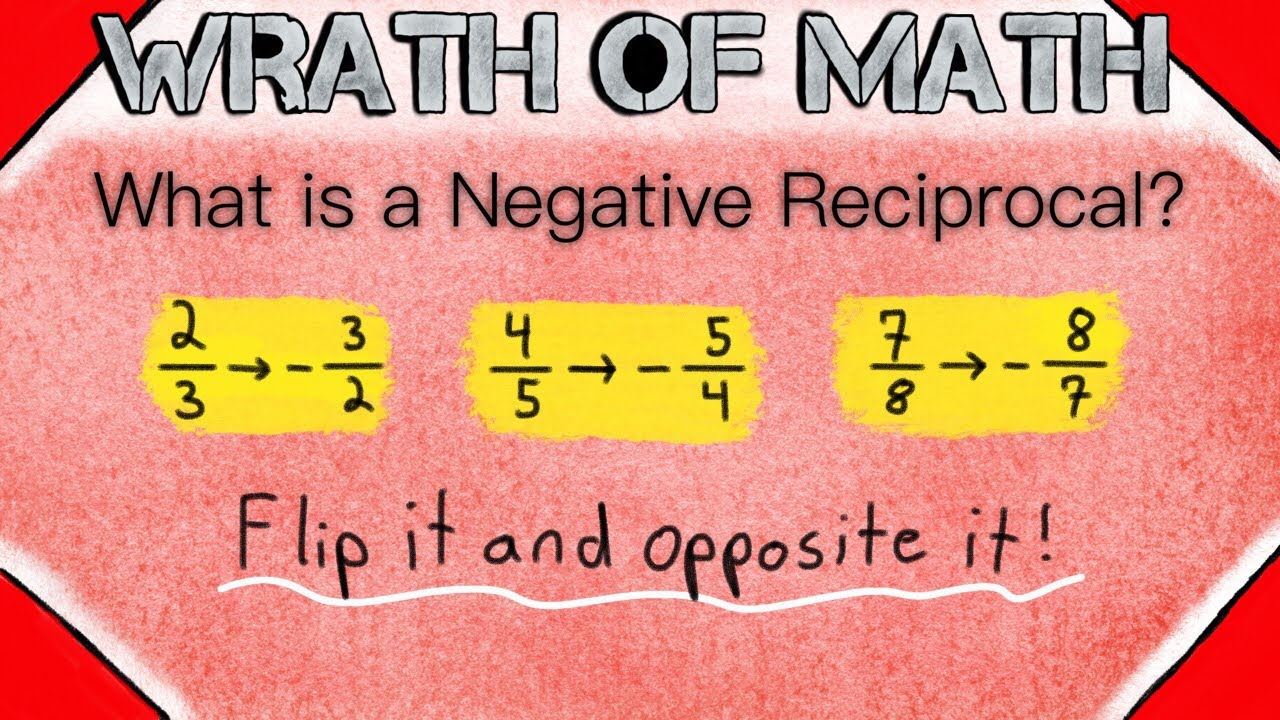Negative Reciprocal: Your Practical Guide & Examples

In mathematics, understanding the negative reciprocal is crucial, especially when dealing with perpendicular lines in coordinate geometry and slope calculations, typically taught within educational curricula. For example, a line with a slope of 2 has a negative reciprocal slope of -1/2. Moreover, functions exhibiting inverse relationships, like those often analyzed using tools from Khan Academy, demonstrate mathematical principles closely tied to the concept of the negative reciprocal, as inverse transformations alter the original value. Specifically, if a function's slope is defined, the negative reciprocal can predict the behavior of a line that intersects the original at a right angle, a principle also applied in fields that rely on spatial mathematics.

Image taken from the YouTube channel David May , from the video titled What is a Negative Reciprocal? | Dave May Teaches .

Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if two lines are perpendicular, meaning they intersect at a right angle (90 degrees). This section will break down what negative reciprocals are and why they are so important.

Defining Reciprocals: The Foundation

The reciprocal of a number is simply 1 divided by that number. It's also commonly referred to as "flipping" the fraction.

For instance, the reciprocal of 2 is 1/2. If you start with a fraction, like 3/4, its reciprocal is 4/3. Multiplying a number by its reciprocal always results in 1, which is a core principle to remember.

Negative Reciprocals: Adding the "Negative" Twist

A negative reciprocal takes the concept of a reciprocal a step further by introducing a negative sign. To find the negative reciprocal of a number, you first find its reciprocal and then change its sign.

For example, the reciprocal of 2 is 1/2, and therefore the negative reciprocal of 2 is -1/2. Similarly, the reciprocal of -3/4 is -4/3, so the negative reciprocal is 4/3.

Understanding this process is key to unlocking the relationship with perpendicularity.

The Connection to Perpendicularity: The Core Concept

The most significant application of negative reciprocals lies in identifying perpendicular lines. Two lines are perpendicular if and only if the product of their slopes is -1. This means their slopes are negative reciprocals of each other.

In simpler terms:

• If one line has a slope of m, a line perpendicular to it will have a slope of -1/m.

This relationship is not arbitrary; it's a direct consequence of the geometric properties of right angles and how slopes define the direction of a line. It’s the core rule we use to solve perpendicularity problems.

Real-World Relevance: Where Does It Matter?

The concept of perpendicularity, and therefore negative reciprocals, is far from abstract. It has widespread applications in various fields.

In construction, ensuring walls are perpendicular is crucial for structural integrity. In architecture, precise angles are essential for both aesthetics and functionality.

Design, whether it's graphic or industrial, relies heavily on understanding angles and spatial relationships. Even in fields like navigation and mapping, perpendicularity plays a role in determining accurate directions and positions.

Therefore, a solid grasp of negative reciprocals provides a valuable tool for analyzing and solving real-world problems beyond the classroom.

Understanding Slope: Rise Over Run and Its Significance

Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if two lines are perpendicular, meaning they intersect at a right angle (90 degrees). This section will break down what negative reciprocals are and why they are so important.

Defining Slope: The Foundation of Linearity

At its core, slope describes the steepness and direction of a line. It's a fundamental concept in understanding linear relationships. We often express slope as "rise over run," a ratio that quantifies how much a line changes vertically (the "rise") for every unit of horizontal change (the "run").

Imagine a line climbing a hill. The "rise" is how much higher you get, and the "run" is how far you walked horizontally to get there. The slope is the ratio of these two values.

Mathematically, if we have two points on a line, (x₁, y₁) and (x₂, y₂), the slope (often denoted as 'm') is calculated as:

m = (y₂ - y₁) / (x₂ - x₁)

This formula provides a precise way to determine the slope from any two points on the line. It's a cornerstone of linear algebra and coordinate geometry.

Types of Slopes: A Visual Guide

Lines can have various types of slopes, each with its distinct visual representation:

• Positive Slope: A line with a positive slope rises as you move from left to right. It indicates a direct relationship; as x increases, y also increases. Think of climbing a hill.

• Negative Slope: A line with a negative slope falls as you move from left to right. This indicates an inverse relationship; as x increases, y decreases. Think of descending a hill.

• Zero Slope: A horizontal line has a slope of zero. This means that the value of y remains constant regardless of the value of x. It's a flat, level surface.

• Undefined Slope: A vertical line has an undefined slope. This is because the "run" is zero, leading to division by zero in the slope formula. The value of x remains constant, regardless of the value of y.

Understanding these slope types is crucial for interpreting graphs and understanding the relationship between variables.

The Variable "m": Slope's Algebraic Identity

In mathematical equations, the slope is almost universally represented by the variable "m". This convention stems from the French word "monter," meaning "to climb" or "to ascend."

The use of 'm' is deeply ingrained in mathematical notation. You'll see it used in various forms of linear equations, such as the slope-intercept form (y = mx + b), where 'm' is the coefficient of x, directly indicating the slope of the line.

Relating Slope to Lines: Steepness and Direction

The value of the slope directly determines both the steepness and the direction of a line. The larger the absolute value of the slope, the steeper the line.

A slope of 2 is steeper than a slope of 1.

The sign of the slope indicates the direction: positive for an upward slant, negative for a downward slant.

A line with a slope of -3 is steeper and slopes downwards compared to a line with a slope of -1. Understanding how slope translates to visual characteristics is vital for interpreting and creating accurate graphical representations of linear equations.

Perpendicular Lines: Where Right Angles Reign Supreme

Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if two lines are perpendicular, meaning they intersect at a right angle (90 degrees). This section will break down what makes lines perpendicular and why negative reciprocals are so important.

Defining Perpendicularity: The Essence of a Right Angle

Perpendicular lines are defined by a specific geometric property: they intersect at a right angle. A right angle is, quite simply, an angle that measures exactly 90 degrees.

It's this precise angular relationship that makes perpendicularity so important in various applications. When two lines meet perfectly to form that 'L' shape, we know we're dealing with perpendicularity.

Real-World Examples: Perpendicularity All Around Us

Perpendicular lines aren't confined to textbooks; they are all around us in the world. Consider the corners of a room: the walls typically meet the floor (or ceiling) at right angles.

Think about the streets in a well-planned city grid, where avenues run perpendicular to streets, creating clear and organized intersections.

Doors and windows are rectangles, and these are made up of perpendicular lines. Picture the crosshairs of a scope on a rifle, or a navigation system. Even the way we hold our tools: perpendicularity is a fundamental aspect of our designed world.

The Negative Reciprocal Rule: The Slope Connection

The critical link between negative reciprocals and perpendicularity lies in the slopes of the lines.

Two lines are perpendicular if and only if the product of their slopes equals -1.

This is often stated as: two lines are perpendicular if and only if their slopes are negative reciprocals of each other. Mathematically, if one line has a slope of m₁ and another has a slope of m₂, they are perpendicular if m₁ m₂ = -1.

Consider a line with a slope of 2. Its negative reciprocal is -1/2. If another line has a slope of -1/2, it is perpendicular to the original line.

The Symbol of Perpendicularity: ⊥

In mathematical notation, perpendicularity is represented by the symbol "⊥".

So, if line AB is perpendicular to line CD, we write it as AB ⊥ CD. This symbol offers a concise way to express the relationship between lines, angles, planes, and even vectors.

It is a shorthand notation used in geometry, trigonometry, and calculus. This is especially useful in proofs and complex problems, where visualizing relationships are paramount.

Linear Equations and Their Slopes: Extracting Key Information

Perpendicular lines: Where Right Angles Reign Supreme Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if two lines are perpendicular, meaning they intersect at a right angle (90 degrees). This section will break down what makes negative reciprocals so important for understanding lines.

This section delves into the practical application of negative reciprocals by exploring how to extract slope information from different forms of linear equations. Mastering this skill is essential for determining if lines are perpendicular. We’ll explore how to identify the slope within various forms and how to calculate the slope of a line perpendicular to it.

Slope-Intercept Form: Decoding the Equation

The slope-intercept form of a linear equation, y = mx + b, is arguably the most straightforward when it comes to identifying the slope.

In this form, 'm' directly represents the slope of the line, and 'b' represents the y-intercept (the point where the line crosses the y-axis).

For example, in the equation y = 3x + 2, the slope is simply 3.

Identifying 'm' in this form is a direct read. This is often the starting point for grasping the relationship between an equation and its visual representation.

Point-Slope Form: Building Equations from a Point and Slope

The point-slope form, y - y₁ = m(x - x₁), is useful when you know a point on the line (x₁, y₁) and the slope 'm'.

While 'm' is still readily identifiable, this form's power lies in its ability to construct the equation of a line given specific conditions.

Imagine you want to find the equation of a line perpendicular to another, and you know it passes through the point (2, -1). First, find the slope of the perpendicular line by taking the negative reciprocal of the original line's slope. Then, plug the point and the new slope directly into the point-slope form to build your equation.

This form emphasizes that a line is uniquely defined by its direction (slope) and a single point it passes through.

Standard Form: Unveiling the Slope

The standard form of a linear equation, Ax + By = C, doesn't explicitly reveal the slope. However, it’s still possible to find it.

One way is to convert the equation into slope-intercept form by solving for y.

Alternatively, a quick formula can be used: m = -A/B.

For instance, given the equation 2x + 3y = 6, the slope is m = -2/3. It requires a little algebraic manipulation but is a very useful trick to have.

Finding Perpendicular Slopes: Applying the Negative Reciprocal

The core concept: two lines are perpendicular if and only if the product of their slopes is -1. This translates to finding the negative reciprocal.

To find the slope of a line perpendicular to another, simply flip the fraction and change the sign.

For example:

• If the slope of a line is 2 (or 2/1), the slope of a perpendicular line is -1/2.
• If the slope is -3/4, the perpendicular slope is 4/3.

Regardless of the form of the original equation, once you've identified the slope, finding the perpendicular slope is a straightforward application of the negative reciprocal. Mastering this skill allows you to confidently navigate problems involving perpendicular lines.

Connecting to Right Angles: The Foundation of Perpendicularity

Linear Equations and Their Slopes: Extracting Key Information Perpendicular lines: Where Right Angles Reign Supreme Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if two lines are perpendicular, meaning they intersect at a right angle. Let's delve deeper into this connection, solidifying the geometrical understanding of how perpendicularity relates to right angles.

Understanding Right Angles

At the heart of perpendicularity lies the right angle. It's a fundamental concept in geometry, serving as a building block for more complex shapes and calculations.

A right angle is defined as an angle that measures precisely 90 degrees. It's often represented by a small square at the vertex of the angle.

Recognizing right angles is essential, as they are ubiquitous in our world, from the corners of buildings to the edges of books.

Perpendicular Lines: The Creators of Right Angles

Perpendicular lines are defined as two lines that intersect each other, forming right angles at their point of intersection.

This relationship is absolute and unwavering; whenever two lines are perpendicular, they will invariably create right angles.

This is a key principle to internalize, forming the cornerstone of understanding how negative reciprocals are so important in geometry.

Right Triangles and the Pythagorean Theorem

The relationship between perpendicular lines and right angles extends to the realm of triangles.

When a transversal line intersects two perpendicular lines, a right triangle is formed.

This is where the famous Pythagorean Theorem comes into play. The Pythagorean Theorem is a powerful relationship that defines a relationship in any triangle with a ninety-degree angle, mathematically.

The theorem states: a² + b² = c², where 'a' and 'b' are the lengths of the two sides forming the right angle, and 'c' is the length of the hypotenuse (the side opposite the right angle).

In this context, the perpendicular lines (sides 'a' and 'b') directly contribute to determining the length of the hypotenuse.

Visualizing Perpendicularity and Right Angles

To solidify your understanding, consider a visual example: Imagine two lines on a graph, one running horizontally and the other vertically, intersecting at the origin (0,0).

The angle formed at the intersection is a clear 90-degree right angle. Now, picture a third line connecting points on these two lines, creating a right triangle.

This visual reinforces how perpendicular lines are integral in forming right angles and right triangles. Using online graphing tools like Desmos or GeoGebra, you can draw these shapes and visually confirm the principles described.

By understanding these fundamental connections, we can now move forward to exploring the more in-depth relationships between the negative reciprocals of linear equations in the sections that follow.

Working with Fractions and Integers: Mastering the Mechanics

Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if lines are perpendicular. But the process of finding these reciprocals can sometimes feel tricky, especially when you're working with fractions, integers, or even the seemingly simple case of zero. This section provides practical guidance on how to master the mechanics of finding negative reciprocals, building your confidence and accuracy in this essential skill.

The Negative Reciprocal of a Fraction: Flip and Change

The key to finding the negative reciprocal of a fraction lies in two simple steps: flipping the fraction (inverting the numerator and denominator) and changing its sign. Let's break that down:

First, consider the fraction 2/3. To find its reciprocal, we simply swap the numerator and denominator, resulting in 3/2.

Next, we address the sign. If the original fraction was positive, we make the reciprocal negative. Conversely, if the original fraction was negative, the reciprocal becomes positive.

Therefore, the negative reciprocal of 2/3 is -3/2.

Let's look at another example: what's the negative reciprocal of -5/7? We flip the fraction to get 7/5. Since the original fraction was negative, the negative reciprocal is positive, giving us 7/5.

This process, while straightforward, is the bedrock for many calculations involving perpendicular lines.

Integers: The Invisible Denominator

Integers might seem different from fractions at first glance, but remember that any integer can be expressed as a fraction with a denominator of 1.

For instance, the integer 5 can be written as 5/1. Now, finding the negative reciprocal becomes a familiar process.

We flip the fraction to get 1/5, and then change the sign. Since 5 was positive, its negative reciprocal is -1/5.

Similarly, the integer -3 can be expressed as -3/1. Flipping it gives us 1/-3, which simplifies to -1/3. Changing the sign, we see it will be converted to the + form, but because it simplifies to begin with it becomes negative regardless.

Therefore, the negative reciprocal of -3 is 1/3.

By understanding this simple conversion, you can confidently handle integers when working with negative reciprocals.

The Peculiarity of Zero: An Undefined Reciprocal

When it comes to reciprocals, zero is a special case. The reciprocal of a number is found by dividing 1 by that number. So, the reciprocal of zero would be 1/0.

However, division by zero is undefined in mathematics. This means that zero simply does not have a reciprocal, and therefore, it also doesn't have a negative reciprocal.

This exception is important to remember. When dealing with slopes, a slope of zero represents a horizontal line. A line perpendicular to a horizontal line is a vertical line, which has an undefined slope. This reflects the fact that zero's reciprocal is undefined.

Edge Cases: 1 and -1

Finally, let's consider the edge cases of 1 and -1. These numbers have unique properties when it comes to reciprocals.

The reciprocal of 1 is 1/1, which simplifies to 1. Therefore, the negative reciprocal of 1 is -1.

Similarly, the reciprocal of -1 is 1/-1, which simplifies to -1. The negative reciprocal of -1 is therefore 1.

In essence, the negative reciprocals of 1 and -1 are simply their opposites. These are important to note for unique instances when graphing and when calculating relationships between slopes. They are values, however, and do still exist in the negative reciprocal plane.

Visualizing on the Coordinate Plane: Seeing is Believing

Working with Fractions and Integers: Mastering the Mechanics Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if lines are perpendicular. But the process of finding these reciprocals can sometimes feel tricky, especially when you’ve worked through the calculations.

That's where the coordinate plane comes in, offering a powerful way to visually confirm and solidify your understanding. By plotting lines and observing their relationships, you can gain an intuitive grasp of how negative reciprocals govern perpendicularity.

Graphing Lines: Bringing Equations to Life

The coordinate plane, also known as the Cartesian plane, provides a visual landscape for linear equations. To graph a line, you first need its equation, typically in slope-intercept form (y = mx + b).

The 'm' value represents the slope, and 'b' is the y-intercept (where the line crosses the y-axis).

Plot at least two points that satisfy the equation and then draw a straight line through them. Choose a point with coordinate (x,y) where 'x' and 'y' values satisfy the condition when plugged into the linear equation.

It may be helpful to find points near the edges of the graph, as it helps with visualizing the position of the line over the entire grid.

Repeat this process for a second equation, and the relationship between the two lines will become clear.

Visually Verifying Perpendicularity

Once you have graphed two lines, there are a couple of ways to visually check if they are perpendicular.

• Right Angle Observation: Look at the point where the lines intersect. If the angle formed appears to be a right angle (90 degrees), it's a good indication that the lines are indeed perpendicular.

  • You can often visually approximate a right angle fairly well, but for precise confirmation, use a protractor.

• Using a Protractor: For a more accurate assessment, use a protractor to measure the angle between the lines.

  • If the angle measures 90 degrees, you have visual confirmation that the lines are perpendicular.

Impact of Slope Changes: Dynamic Confirmation

Experimenting with different slope values provides further insight into the negative reciprocal relationship.

• Steeper Slopes: Increasing the absolute value of the slope ('m') makes the line steeper.

  • A positive slope indicates an upward slant from left to right, while a negative slope indicates a downward slant.
• Observing Orientation: By changing the slope of one line and observing how it affects its orientation relative to another line, you can see how the negative reciprocal relationship ensures perpendicularity.

• Parallel lines: If two lines have equal slopes, they never intersect and run parallel to one another.

  • Visually recognizing that these lines will never intercept, also allows us to visualize that they cannot possibly be perpendicular.

Coordinate Examples: Quantifying the Visual

Let's put this into practice with a concrete example. Consider two lines:

• Line 1 passes through points (1, 2) and (3, 6).
• Line 2 passes through points (4, 4) and (6, 3).

To determine if these lines are perpendicular, let's calculate their slopes.

Calculating Slopes

Recall that slope (m) is calculated as: m = (y2 - y1) / (x2 - x1)

• Slope of Line 1: m1 = (6 - 2) / (3 - 1) = 4 / 2 = 2
• Slope of Line 2: m2 = (3 - 4) / (6 - 4) = -1 / 2 = -1/2

Checking for Perpendicularity

Now, let's check if the slopes are negative reciprocals of each other. Is -1/2 the negative reciprocal of 2? Yes, it is!

We can confirm that 2 * (-1/2) = -1, so the lines are perpendicular.

Plotting these points and drawing the lines on a coordinate plane will visually confirm this relationship.

Geometry: Exploring Negative Reciprocals in Shapes and Proofs

Visualizing on the Coordinate Plane: Seeing is Believing Working with Fractions and Integers: Mastering the Mechanics Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if lines are perpendicular. But the process of finding these reciprocals and applying them extends beyond simple calculations; it forms a cornerstone of geometric reasoning and proof.

This section delves into how negative reciprocals are used in formal geometric proofs, constructions, and understanding the intrinsic properties of familiar shapes. The concept moves from the abstract to the tangible, allowing for a deeper, more intuitive grasp of its importance.

The Power of Negative Reciprocals in Geometric Proofs

Geometric proofs often rely on establishing relationships between lines and angles. Proving that two lines are perpendicular is a common goal. This is where the concept of negative reciprocals becomes invaluable.

If you can demonstrate that the slopes of two lines are negative reciprocals of each other, you've proven, without a doubt, that they are perpendicular. This provides a powerful tool for deductive reasoning, solidifying the logical structure of the proof.

For instance, imagine a proof where you've calculated the slopes of two line segments within a complex figure. If these slopes turn out to be, say, 2/3 and -3/2, you can immediately state that these lines are perpendicular based on the negative reciprocal theorem.

This approach avoids the need for direct angle measurement, making the proof process cleaner and more efficient.

Constructing Perpendicular Lines with Precision

Beyond proofs, negative reciprocals guide precise geometric constructions. Using only a compass and straightedge, we can construct perpendicular lines based on established geometric principles.

One common method involves creating a perpendicular bisector of a line segment. This bisector, by definition, is perpendicular to the original segment.

While the construction itself doesn't directly calculate the negative reciprocal, the underlying principle ensures that the resulting lines meet at a perfect right angle. This exemplifies how theoretical knowledge translates into practical construction techniques.

Applications in Understanding Shapes and Figures

Negative reciprocals also play a critical role in understanding the properties of many geometric shapes. Squares, rectangles, and right triangles all inherently rely on the concept of perpendicularity.

• Squares and Rectangles: These quadrilaterals are defined by having four right angles. Therefore, adjacent sides of these shapes must have slopes that are negative reciprocals of each other.

• Right Triangles: By definition, one angle in a right triangle is 90 degrees. The two sides forming this angle are perpendicular, and their slopes are, again, negative reciprocals.

Understanding this connection allows us to quickly identify and classify shapes based on the slopes of their sides. It also allows us to solve more complicated geometric problems, with the knowledge of the exact angles.

Shape Examples: Visualizing the Relationship

Let's consider a few specific examples to solidify this understanding:

• Example 1: Square ABCD: Suppose side AB has a slope of 1. If ABCD is a square, then side BC (which is perpendicular to AB) must have a slope of -1.

• Example 2: Rectangle EFGH: If side EF has a slope of -1/2, then side FG must have a slope of 2 to form a right angle at vertex F.

• Example 3: Right Triangle XYZ: If the leg XY has a slope of 4, the leg YZ (perpendicular to XY) has a slope of -1/4. The application of the formula here allows us to better describe the shape, and the space it takes up.

By visualizing these relationships on a coordinate plane, we can gain a more intuitive understanding of how negative reciprocals govern the geometry of these fundamental shapes. The connection between algebra and geometry becomes beautifully apparent, empowering us to analyze and solve geometric problems with increased confidence.

Real-World Applications: Where Math Meets the World

Negative reciprocals are a foundational concept in mathematics, especially when dealing with lines and their orientations. Understanding them is crucial for determining if lines are perpendicular, a relationship that manifests extensively in the world around us. Let's explore how this seemingly abstract mathematical principle directly impacts various practical fields.

Architecture: Building on Right Angles

Architecture relies heavily on precise angles and spatial relationships. Perpendicularity is fundamental to building design, ensuring structural stability and aesthetic appeal. Architects use negative reciprocals to guarantee that walls meet at perfect right angles, forming the very foundation of habitable spaces.

For example, when designing a rectangular room, architects must ensure that the walls are perpendicular to the floor and to each other. This is achieved by calculating the slopes of the lines representing the walls and ensuring their slopes are negative reciprocals. This guarantees a perfect 90-degree angle.

Furthermore, negative reciprocals play a role in calculating roof pitches. The steepness of a roof affects its ability to shed water and snow, and also influences the overall aesthetic of the building. These slopes, when intersecting, need to be at precise angles, often derived using negative reciprocal relationships.

Engineering: Structural Integrity and Force Vectors

Engineering, particularly civil and mechanical engineering, demands a rigorous understanding of forces and structures. Negative reciprocals are instrumental in calculating these.

In structural design, engineers use negative reciprocals to ensure that supporting beams and columns are perpendicular to the ground, providing maximum stability. This is critical for bridges, buildings, and other infrastructure projects.

Consider a bridge design: the support pillars must be precisely perpendicular to the bridge deck to evenly distribute the load. Any deviation from a right angle can compromise the structural integrity and lead to catastrophic failure.

Mechanical engineers utilize negative reciprocals in force calculations. When analyzing forces acting on an object, engineers often resolve these forces into perpendicular components. The relationships between these components, including their slopes and angles, are often governed by the principles of negative reciprocals, ensuring accurate and safe designs.

Navigation: Charting the Course

While less obvious, navigation systems also rely on the principles underpinning negative reciprocals.

On maps, lines representing courses and bearings are often analyzed using coordinate geometry. Determining if one route is perpendicular to another, or calculating angles for course corrections, necessitates an understanding of slope and negative reciprocal relationships.

Furthermore, modern GPS systems rely on complex mathematical algorithms to determine location and direction. These algorithms often use coordinate geometry and vector calculations. Calculating angles and distances relative to reference points involves implicit application of negative reciprocal concepts, ensuring precise and reliable navigation.

Construction: Laying the Foundation for Accuracy

Construction workers apply the principles derived from negative reciprocals directly in setting foundations, framing walls, and ensuring overall structural accuracy.

When laying a foundation, it is crucial to establish a level and perpendicular base. This is achieved using tools like levels and squares, but also through mathematical calculations. By verifying that the lines representing the edges of the foundation have slopes that are negative reciprocals of each other, builders can guarantee that the foundation is square and true.

Framing walls involves ensuring that the studs are perpendicular to the floor and ceiling. This again necessitates a practical understanding of right angles, which are mathematically represented by the negative reciprocal relationship of the slopes of intersecting lines. Precise construction using these relationships is what ensures a sound, stable, and safe structure.

In essence, the concept of negative reciprocals transcends the realm of abstract mathematics. It serves as a cornerstone in architecture, engineering, navigation, and construction. It ensures structures are sound, designs are accurate, and systems operate reliably. This mathematical principle is a silent but essential contributor to the built world we inhabit.

Online Graphing Tools: A Powerful Visualization Aid

Visualizing mathematical concepts can often be the key to truly understanding them. While formulas and equations provide the framework, seeing how these concepts translate into graphical representations solidifies the knowledge.

Fortunately, numerous online graphing tools are available today that can dramatically enhance this learning process. These tools empower students, educators, and professionals alike to explore and verify mathematical principles with unprecedented ease.

Desmos and GeoGebra: Top Choices for Visual Learning

When it comes to online graphing, Desmos and GeoGebra stand out as exceptional resources. Both offer intuitive interfaces and powerful features that make them ideal for visualizing linear equations, exploring slopes, and investigating the relationship between negative reciprocals and perpendicularity.

Desmos is known for its clean design and user-friendly experience, making it incredibly accessible even for beginners. GeoGebra, on the other hand, offers a broader range of functionalities, catering to more advanced mathematical explorations.

Ultimately, the best choice depends on individual needs and preferences. But both platforms provide an invaluable service to anyone seeking a visual understanding of mathematical concepts.

Interactive Manipulation: See Concepts in Action

One of the greatest strengths of these online graphing tools is their interactive nature. Users can directly manipulate equations, change parameters, and observe in real-time how these adjustments affect the graphical representation.

For example, students can alter the slope of a line and instantly see how its steepness and direction change. This interactive experience allows for a much deeper and more intuitive understanding of the relationship between equations and their corresponding graphs.

By dragging points, adjusting coefficients, or modifying functions, users can explore a wide range of scenarios and gain insights that would be difficult to achieve through static diagrams or traditional textbook examples.

Verifying Calculations and Predictions

Online graphing tools are not just for exploration; they are also powerful tools for verification. After manually calculating the slope of a line or predicting whether two lines are perpendicular, users can graph the equations and visually confirm their results.

This process reinforces understanding and helps to identify potential errors in calculations. It also builds confidence in one's ability to apply mathematical concepts correctly.

By comparing predicted outcomes with actual graphical representations, learners can strengthen their problem-solving skills and develop a deeper appreciation for the accuracy and consistency of mathematical principles.

Leveraging Tool-Specific Features

Both Desmos and GeoGebra offer a range of features that are particularly useful for exploring perpendicularity and negative reciprocals.

• Angle Measurement: Both tools can measure angles, allowing users to directly verify that perpendicular lines form right angles (90 degrees).

  This visual confirmation reinforces the connection between perpendicularity and right angles, making the concept more concrete.

• Slope Calculation: Users can often select two points on a line, and the tool will automatically calculate the slope.

  This feature saves time and reduces the risk of calculation errors, allowing students to focus on understanding the underlying concepts.

  It also enables users to explore how the slope relates to the coordinates of points on the line.

• Dynamic Construction: GeoGebra, in particular, allows for dynamic geometric constructions. Users can create perpendicular lines and explore their properties by manipulating the construction.

  This feature offers a powerful way to investigate the geometric relationships between lines, angles, and shapes.

By taking advantage of these tool-specific features, users can gain a richer and more nuanced understanding of negative reciprocals and their role in determining perpendicularity.

Video: Negative Reciprocal: Your Practical Guide & Examples

Play Video

So, next time you're staring at a graph or trying to figure out if those walls are really perpendicular, remember your friend, the negative reciprocal! It's a handy little trick that can save you a lot of time and frustration. Go forth and conquer those lines!