Standard Deviation Unit: Simple Guide You Must Know!

The **concept of variability**, a cornerstone in statistical analysis, is best measured using the standard deviation unit. **Finance professionals** at institutions like BlackRock, frequently employ the standard deviation unit to assess portfolio risk. This metric’s calculation, often performed using tools like **Microsoft Excel**, provides crucial insights into data spread. Understanding the standard deviation unit is paramount for anyone seeking to interpret and apply statistical data meaningfully.

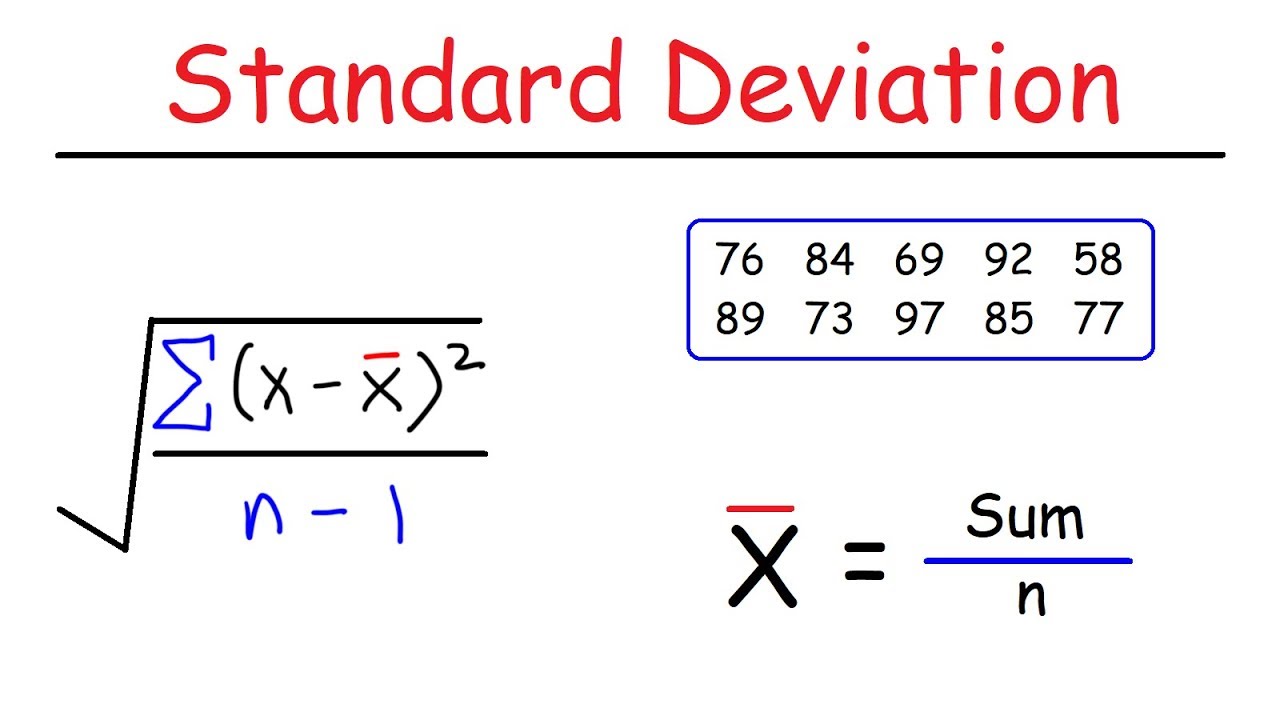
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled How To Calculate The Standard Deviation .

In the realm of statistics, where data reigns supreme, understanding the dispersion of that data is just as crucial as knowing its central tendency. Enter standard deviation: a fundamental concept that unlocks deeper insights into the nature and behavior of datasets.

This article serves as your straightforward guide to grasping the standard deviation unit, demystifying its calculation and interpretation. We aim to empower you with the knowledge necessary to confidently analyze data and draw meaningful conclusions.

What is Standard Deviation? A Concise Definition

At its core, standard deviation is a measure of how spread out numbers are in a dataset. More formally, it quantifies the average distance of individual data points from the mean (average) of the dataset.

A low standard deviation indicates that the data points tend to be clustered closely around the mean, suggesting consistency and stability. Conversely, a high standard deviation signals that the data points are more dispersed, indicating greater variability.

Standard deviation helps to determine the reliability of statistical conclusions. By understanding the measure of spread, data analysts can determine the confidence level of the statistical outcomes.

Why Standard Deviation Matters: The Key to Effective Data Analysis

Comprehending standard deviation is not merely an academic exercise; it's a vital skill for anyone working with data. It provides a critical lens through which to interpret statistical findings, assess risk, and make informed decisions.

Without understanding how data is distributed, we risk misinterpreting averages, overlooking critical outliers, and drawing inaccurate conclusions. Standard deviation, therefore, acts as a safeguard against such errors, enabling more robust and reliable analysis.

Standard deviation enables powerful data analysis, helping the analyzer to determine the degree to which the data varies from the expected outcome. With that, key data insights can be extracted to further improve business processes.

Whether you're a student, researcher, business analyst, or simply a data enthusiast, mastering standard deviation will significantly enhance your ability to extract meaningful insights from data and make well-informed decisions.

Standard deviation, therefore, acts as a crucial benchmark against which we measure the consistency and predictability of data, allowing us to move from simply observing values to truly understanding the patterns they reveal. With the importance of standard deviation established, let’s break down the fundamental concepts that make up this powerful statistical tool, clarifying its relationship to other key measures like variance and the mean.

Decoding the Fundamentals: What You Need to Know

To effectively wield standard deviation, we must first understand its components and how it relates to other statistical measures. This section will define standard deviation, explore its connection to the mean and variance, and explain how it quantifies data dispersion.

Defining Standard Deviation

Standard deviation, at its core, is a measure of the spread or dispersion within a dataset. It tells us how much individual data points deviate from the "typical" value, which is represented by the mean.

Think of the mean as the balancing point of a dataset. Standard deviation then, measures the average distance of each data point from that balancing point.

A low standard deviation indicates that the data points tend to be clustered closely around the mean, suggesting consistency and stability.

Conversely, a high standard deviation signals that the data points are more dispersed, indicating greater variability. Understanding this spread is crucial for interpreting the true nature of the data.

Standard Deviation's Relationship to the Mean

The mean, or average, is a fundamental concept in statistics, representing the central tendency of a dataset. Standard deviation builds upon this concept by measuring the spread of data relative to the mean.

It quantifies, in a single number, how much the individual data points differ, on average, from the mean.

The mean acts as the reference point, and the standard deviation tells us how far, on average, the data points are scattered around that reference point.

This relationship is essential because it allows us to understand not just the central value of the data, but also its typical range and variability.

Variance: The Foundation of Standard Deviation

Variance is another key concept intimately related to standard deviation. In fact, variance is the square of the standard deviation.

It measures the average squared deviation from the mean. This means that each data point's difference from the mean is squared, and then these squared differences are averaged.

Squaring the deviations ensures that all deviations are positive, preventing negative and positive deviations from canceling each other out.

While variance provides a measure of data spread, it's expressed in squared units, which can be difficult to interpret directly. This is where standard deviation comes in.

Standard deviation is simply the square root of the variance, bringing the measure of spread back into the original units of the data. Variance serves as an intermediate step in calculating standard deviation, providing a necessary mathematical foundation for understanding data dispersion. By understanding variance, we can better appreciate the meaning and calculation of standard deviation.

Standard deviation, therefore, acts as a crucial benchmark against which we measure the consistency and predictability of data, allowing us to move from simply observing values to truly understanding the patterns they reveal. With the importance of standard deviation established, let’s break down the fundamental concepts that make up this powerful statistical tool, clarifying its relationship to other key measures like variance and the mean.

Calculating Standard Deviation: A Step-by-Step Guide

Now that we've established the foundational concepts of standard deviation, it's time to put theory into practice. This section will serve as a practical guide, walking you through the calculation of standard deviation for both populations and samples.

Understanding the nuances of each calculation is crucial for accurate data analysis. We’ll dissect the formulas, define each component, and illustrate the process with clear, step-by-step examples.

Standard Deviation for a Population: A Complete Walkthrough

When working with data representing an entire population, the standard deviation calculation aims to provide a comprehensive measure of dispersion. Let's explore the formula and its application.

The Population Standard Deviation Formula

The formula for calculating standard deviation (σ) for a population is expressed as:

σ = √[ Σ (xᵢ - μ)² / N ]

Where:

• σ (sigma): Represents the population standard deviation, the value we aim to calculate.
• Σ (sigma): This symbol denotes summation, meaning we need to add up a series of values.
• xᵢ: Represents each individual data point in the population dataset.
• μ (mu): Represents the population mean, calculated by summing all data points and dividing by the total number of data points (N).
• N: Represents the total number of data points in the population.

Decoding the Formula: A Step-by-Step Breakdown

Let's break down the formula into manageable steps:

1. Calculate the Mean (μ): First, determine the average of your entire population dataset. This involves summing all the values and dividing by the number of values. The mean serves as the central point around which we measure dispersion.

2. Calculate the Deviations (xᵢ - μ): For each data point, subtract the population mean (μ). This calculates how far each value deviates from the average. Some deviations will be positive, and some will be negative.

3. Square the Deviations (xᵢ - μ)²: Square each of the deviations calculated in the previous step. Squaring the deviations ensures that all values are positive, preventing negative and positive deviations from canceling each other out and providing a more accurate measure of overall dispersion.

4. Sum the Squared Deviations (Σ (xᵢ - μ)²): Add up all the squared deviations. This summation provides a total measure of the overall squared dispersion in the dataset.

5. Divide by the Number of Data Points (Σ (xᵢ - μ)² / N): Divide the sum of the squared deviations by the total number of data points (N) in the population. This gives you the variance, which is the average of the squared deviations.

6. Take the Square Root (√[ Σ (xᵢ - μ)² / N ]): Finally, take the square root of the variance. This yields the population standard deviation (σ), which is expressed in the same units as the original data, making it easier to interpret.

Example Calculation: Population Standard Deviation

Let's consider a small population dataset: 2, 4, 6, 8, 10.

1. Calculate the Mean (μ): (2 + 4 + 6 + 8 + 10) / 5 = 6

2. Calculate the Deviations (xᵢ - μ): -4, -2, 0, 2, 4

3. Square the Deviations (xᵢ - μ)²: 16, 4, 0, 4, 16

4. Sum the Squared Deviations (Σ (xᵢ - μ)²): 16 + 4 + 0 + 4 + 16 = 40

5. Divide by the Number of Data Points (Σ (xᵢ - μ)² / N): 40 / 5 = 8 (This is the variance)

6. Take the Square Root (√[ Σ (xᵢ - μ)² / N ]): √8 ≈ 2.83

Therefore, the standard deviation of this population is approximately 2.83. This tells us that, on average, the data points in this population deviate from the mean by about 2.83 units.

Standard Deviation for a Sample: Addressing Degrees of Freedom

When dealing with a sample (a subset of a larger population), a slight adjustment to the formula is necessary to account for the fact that a sample provides less information than the entire population. This adjustment involves the concept of degrees of freedom.

The Sample Standard Deviation Formula

The formula for calculating standard deviation (s) for a sample is expressed as:

s = √[ Σ (xᵢ - x̄)² / (n-1) ]

Where:

• s: Represents the sample standard deviation.
• Σ: The summation symbol.
• xᵢ: Represents each individual data point in the sample dataset.
• x̄ (x-bar): Represents the sample mean, calculated by summing all data points in the sample and dividing by the number of data points (n).
• n: Represents the total number of data points in the sample.
• (n-1): Represents the degrees of freedom.

Understanding Degrees of Freedom (n-1)

Degrees of freedom reflect the number of independent pieces of information available to estimate a parameter. In the context of sample standard deviation, one degree of freedom is lost because we use the sample mean (x̄) to estimate the population mean (μ).

Because we’re using the sample mean as an estimate, one of the data points isn’t entirely free to vary; it’s constrained by the fact that the mean is already determined. Therefore, we use (n-1) in the denominator to provide a slightly more accurate estimate of the population standard deviation.

Step-by-Step Sample Standard Deviation Calculation

Let's illustrate the calculation with a sample dataset: 3, 5, 7, 9, 11.

1. Calculate the Sample Mean (x̄): (3 + 5 + 7 + 9 + 11) / 5 = 7

2. Calculate the Deviations (xᵢ - x̄): -4, -2, 0, 2, 4

3. Square the Deviations (xᵢ - x̄)²: 16, 4, 0, 4, 16

4. Sum the Squared Deviations (Σ (xᵢ - x̄)²): 16 + 4 + 0 + 4 + 16 = 40

5. Divide by (n-1): 40 / (5-1) = 40 / 4 = 10 (This is the sample variance)

6. Take the Square Root: √10 ≈ 3.16

Therefore, the standard deviation of this sample is approximately 3.16. Notice that this value is slightly higher than the standard deviation we calculated for the population dataset with similar values.

Population vs. Sample: Why the Calculation Differs

The key difference between calculating standard deviation for a population versus a sample lies in the denominator of the formula. For a population, we divide by N, the total number of data points. For a sample, we divide by (n-1), the degrees of freedom.

This adjustment, using (n-1) instead of n when calculating the standard deviation of a sample, is known as Bessel's correction. Bessel's correction accounts for the fact that the sample standard deviation tends to underestimate the population standard deviation.

By dividing by a slightly smaller number (n-1), the sample standard deviation becomes slightly larger, providing a more accurate estimate of the true population standard deviation. In essence, this adjustment acknowledges the uncertainty introduced by working with a subset of the entire population.

While the difference between dividing by N and (n-1) may seem small, it can have a noticeable impact, especially when dealing with small sample sizes. Using the correct formula is essential for accurate statistical analysis and drawing valid conclusions from your data.

Interpreting Standard Deviation: Making Sense of the Numbers

Having mastered the calculation of standard deviation, the next crucial step is understanding what this value actually tells us about our data. It's not merely a number; it's a lens through which we can assess the distribution, consistency, and potential anomalies within a dataset.

Understanding Data Spread Through Standard Deviation

The magnitude of the standard deviation directly reflects the degree of variability within the dataset. Think of it as a measure of "spread-out-ness."

A small standard deviation implies that the data points are clustered relatively closely around the mean. This suggests a high level of consistency and predictability.

Conversely, a large standard deviation indicates that the data is more widely dispersed, suggesting greater variability and potentially lower predictability.

This difference is critical for making informed decisions. For instance, in manufacturing, a small standard deviation in product dimensions indicates consistent quality.

In finance, a large standard deviation in investment returns signals higher risk.

Standard Deviation and the Normal Distribution: A Powerful Connection

Standard deviation finds its most elegant application within the context of the normal distribution, often visualized as a "bell curve".

This distribution is characterized by its symmetry and the concentration of data around the mean. Standard deviation provides the yardstick to measure distances from the mean in a normal distribution.

The most famous application of this connection is the empirical rule (also known as the 68-95-99.7 rule).

This rule states that, for a normal distribution:

• Approximately 68% of the data falls within one standard deviation of the mean.
• Approximately 95% of the data falls within two standard deviations of the mean.
• Approximately 99.7% of the data falls within three standard deviations of the mean.

This rule allows us to quickly estimate the probability of observing a particular value within a dataset. For example, if the average test score is 70 with a standard deviation of 5, about 95% of the scores will fall between 60 and 80.

Identifying Outliers with Standard Deviation: Spotting the Anomalies

Standard deviation is a powerful tool for identifying potential outliers within a dataset. Outliers are data points that lie significantly far from the mean and may indicate errors, anomalies, or genuinely unusual observations.

One common method for outlier detection is using Z-scores.

The Z-score represents the number of standard deviations a particular data point is away from the mean.

It is calculated as:

Z = (xᵢ - μ) / σ

Where:

• xᵢ is the individual data point.
• μ is the mean of the dataset.
• σ is the standard deviation of the dataset.

A Z-score of 2 indicates that the data point is two standard deviations above the mean.

Generally, data points with Z-scores exceeding a certain threshold (e.g., 2 or 3 in absolute value) are considered potential outliers.

It’s important to note that outlier identification is not an exact science and requires careful consideration of the context and potential reasons for the unusual values. Removing outliers without proper justification can distort the analysis.

Real-World Applications: Where Standard Deviation Matters

Having explored the theoretical underpinnings and interpretive power of standard deviation, it’s time to ground our understanding with real-world applications. This isn't just an academic exercise; standard deviation is a vital tool across numerous disciplines, providing crucial insights for decision-making and problem-solving.

Standard Deviation in Finance: Managing Risk and Return

In the world of finance, standard deviation is synonymous with risk. It quantifies the volatility of an investment, indicating how much returns are likely to deviate from the average.

A high standard deviation signifies a riskier investment, where returns can fluctuate dramatically. Conversely, a low standard deviation suggests a more stable and predictable investment.

Investors use standard deviation to compare the risk profiles of different assets. For example, a portfolio manager might use standard deviation to assess whether the potential returns of a high-growth stock justify its increased volatility compared to a more conservative bond fund.

Standard deviation also helps in constructing diversified portfolios. By combining assets with different standard deviations and correlations, investors can potentially reduce overall portfolio risk without sacrificing returns.

Standard Deviation in Science: Ensuring Accuracy and Precision

Scientific research relies heavily on accurate and precise measurements. Standard deviation plays a critical role in assessing the reliability of experimental data.

In experiments, standard deviation quantifies the spread of data points around the mean value. A small standard deviation indicates high precision, suggesting that the measurements are tightly clustered and reproducible.

A large standard deviation, on the other hand, suggests greater variability and potential sources of error. Scientists use standard deviation to identify outliers, validate experimental procedures, and compare results across different studies.

For example, in pharmaceutical research, standard deviation is used to ensure the consistency and efficacy of drug dosages. A low standard deviation in drug potency ensures that each dose delivers the intended therapeutic effect.

Standard Deviation in Data Analytics: Unveiling Patterns and Anomalies

In the age of big data, standard deviation is an indispensable tool for data analysts. It helps to summarize and interpret large datasets, identify patterns, and detect anomalies.

Data analysts use standard deviation to understand the distribution of data points, identify outliers, and assess the significance of statistical findings. For example, in marketing, standard deviation can be used to analyze customer spending patterns.

A high standard deviation in purchase amounts might indicate a diverse customer base with varying spending habits. Identifying these patterns allows for more targeted marketing campaigns.

Standard deviation is also crucial in fraud detection. Unusual transactions that fall far outside the typical range (as measured by standard deviation) can be flagged for further investigation.

Everyday Applications: From Quality Control to Sports Analytics

Beyond finance, science, and data analytics, standard deviation has numerous applications in everyday life. In manufacturing, it ensures product quality by monitoring the consistency of dimensions, weights, and other critical parameters.

In sports analytics, standard deviation helps to evaluate player performance.

For instance, a basketball player with a low standard deviation in scoring demonstrates consistent performance, while a high standard deviation suggests more variability.

Even in education, standard deviation can be used to assess the consistency of student test scores. A small standard deviation indicates that students are performing at a similar level, while a large standard deviation suggests a wider range of abilities.

The Ubiquity of Standard Deviation: A Tool for Understanding Variability

These examples illustrate the versatility and importance of standard deviation as a tool for understanding variability. Whether it's managing financial risk, ensuring scientific accuracy, or uncovering hidden patterns in data, standard deviation provides valuable insights for making informed decisions in a complex and uncertain world. Its applicability extends far beyond the classroom, making it a fundamental concept for anyone seeking to understand and interpret data effectively.

Having explored the practical applications of standard deviation across diverse fields, it’s crucial to turn our attention to potential missteps. While standard deviation is a powerful tool, its misuse can lead to flawed analyses and incorrect conclusions. By understanding these common pitfalls, you can ensure the accurate and effective application of this essential statistical measure.

Avoiding Common Mistakes: Pitfalls and Misconceptions

Standard deviation, despite its straightforward calculation, is often misunderstood and misapplied. Recognizing these common pitfalls is crucial for accurate data analysis and informed decision-making. Let's explore some of the key areas where errors frequently occur.

Misunderstanding the Meaning of Zero Standard Deviation

A standard deviation of zero indicates that all data points in the set are identical. This doesn't necessarily imply the data is unimportant or irrelevant.

It simply means there is no variability within that particular dataset. For instance, if you measure the height of every student in a class and they are all exactly the same height, the standard deviation will be zero. This is a valid, albeit potentially uninteresting, result.

Confusing Standard Deviation with Standard Error

Standard deviation describes the spread of individual data points within a sample or population. Standard error, on the other hand, estimates the variability of a sample statistic (like the mean) across multiple samples drawn from the same population.

Confusing these two can lead to incorrect inferences about the population from which the sample was drawn. Always clarify whether you are examining the dispersion of individual data points or the uncertainty in estimating a population parameter.

Ignoring the Impact of Outliers

Outliers, or extreme values, can significantly inflate the standard deviation. A single outlier can distort the perceived variability of the dataset, leading to misleading interpretations.

Before calculating standard deviation, consider the presence of outliers. Investigate their source and decide whether they should be removed or if their impact should be mitigated using robust statistical methods.

Applying Standard Deviation to Non-Normally Distributed Data

Standard deviation is most readily interpretable when applied to data that roughly follows a normal distribution (the bell curve).

When data is significantly non-normal, the standard deviation may not accurately reflect the typical spread of the data. In such cases, consider using alternative measures of dispersion, such as the interquartile range (IQR), which are less sensitive to extreme values and non-normality.

Assuming Standard Deviation is a Universal Measure of Risk

While standard deviation is often used as a measure of risk in finance, it’s important to recognize its limitations. It quantifies volatility, which is the degree of variation in returns.

However, it doesn't differentiate between upside and downside risk. A high standard deviation could reflect both large gains and large losses. Therefore, relying solely on standard deviation for risk assessment can be misleading. Consider using more comprehensive risk measures, such as downside deviation or value at risk (VaR), to capture different aspects of risk.

Mixing Population and Sample Formulas Incorrectly

As noted previously, the formulas for calculating standard deviation differ slightly depending on whether you're working with a population or a sample. Using the population formula on a sample will underestimate the true standard deviation, as it doesn't account for the reduced variability inherent in a sample.

Conversely, using the sample formula on a population is technically incorrect and unnecessary, though the difference in the final result will be minimal, especially with large populations.

Failing to Consider the Context of the Data

Standard deviation should always be interpreted in the context of the data being analyzed. A "large" or "small" standard deviation is relative to the scale and nature of the data.

For example, a standard deviation of 5 might be considered large for test scores with a maximum of 10, but small for annual incomes measured in thousands of dollars. Always consider the units of measurement and the typical range of values when interpreting standard deviation.

Video: Standard Deviation Unit: Simple Guide You Must Know!

Play Video