What Shape Has the Most Sides? Infinity & Beyond!

The pursuit of understanding what shape has the most sides leads us beyond conventional geometry into the realm of theoretical mathematics, where the concept of an apeirogon represents a polygon with an infinite number of sides. Euclid's foundational work on geometry provides the basis for understanding polygons, yet it is in the exploration of limits and infinity, often discussed at institutions like the Fields Institute, that the notion of infinite sides truly takes shape. Visualizing such shapes requires tools capable of rendering complex mathematical concepts, such as Mathematica, allowing us to approach the abstract idea of a shape with infinite sides.

Image taken from the YouTube channel WatchData , from the video titled Comparison: Name Of Every Shape Up To Infinite Sides .

Unveiling Polygons and the Intrigue of Infinity

Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments.

Think of a humble triangle, a steadfast square, or even the more elaborate architecture of a hexagon. Each is a polygon, defined by its sides, vertices, and angles.

But what happens when we push the boundaries of this definition? What occurs when we imagine a polygon with more and more sides, an ever-increasing complexity?

The Dance with Infinity

Imagine a polygon gaining side after side—a heptagon, an octagon, a nonagon, and beyond. Each new side brings the shape closer to something... different.

The essence of the question then arises: What becomes of a polygon as the number of its sides stretches toward infinity? Does it simply become an impossibly complex shape, or does it transform into something else entirely?

Mathematical and Philosophical Echoes

This seemingly simple question opens doors to fascinating realms of thought. Mathematically, it allows us to explore the concept of limits and approximation, foundational to calculus and analysis.

Philosophically, it challenges our notions of definition and the boundaries of abstract thought. When does a thing cease to be itself, and become something new?

Prepare to embark on a journey where polygons become a gateway to understanding infinity itself.

The Building Blocks: Understanding the Essence of a Polygon

Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments.

Think of a humble triangle, a steadfast square, or even the more elaborate architecture of a hexagon. Each is a polygon, defined by its sides.

But what exactly makes a polygon a polygon? Let's dissect the components to truly understand their essence.

Defining the Polygon: A Foundation

At its core, a polygon is a closed, two-dimensional shape. This "closed" aspect is crucial: imagine drawing a continuous line without lifting your pen, ultimately returning to your starting point. That boundary you've created could be a polygon, provided it is also two-dimensional.

And what creates that boundary? Straight sides! These sides are line segments—portions of a line with defined start and end points—that link together to form the polygon's perimeter.

The Key Components Unveiled

Let's break down the anatomy of a polygon into its fundamental parts: sides, vertices, and angles.

Sides: The Building Blocks

As mentioned, sides are the straight line segments that form the boundary of the polygon. These segments are crucial: no curves allowed! The number of sides directly dictates the type of polygon.

Vertices: Where Sides Converge

A vertex (plural: vertices) is the point where two sides meet. Each vertex is a corner of the polygon. Think of vertices as the “joints” connecting the straight “bones” (sides) of the shape.

Angles: The Measure of Turn

At each vertex, an angle is formed where two sides intersect. This angle measures the “turn” between the two sides. The sum of these interior angles is a key property that varies depending on the number of sides in the polygon.

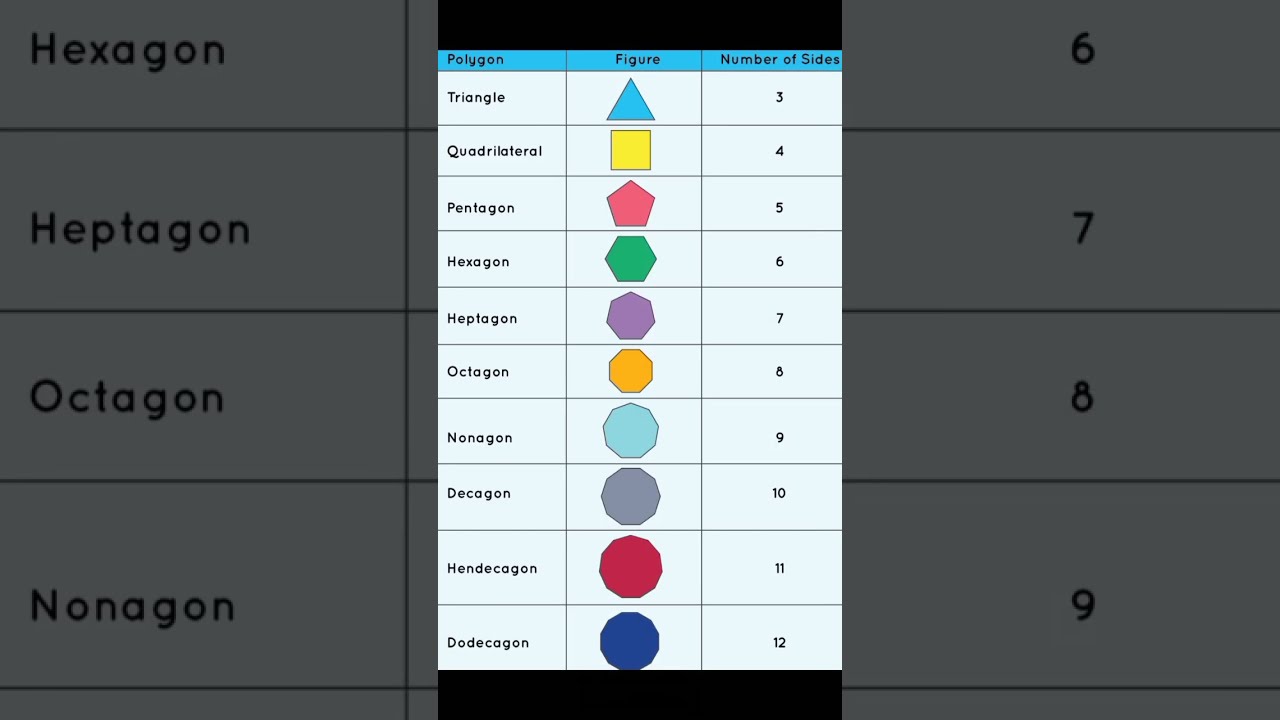
A Polygon Parade: Classifying by Sides

Polygons are classified based on the number of sides they possess:

• Triangle (3 sides): The simplest polygon, forming the basis for many geometric constructions.

• Quadrilateral (4 sides): A versatile group including squares, rectangles, parallelograms, and trapezoids.

• Pentagon (5 sides): Instantly recognizable, think of the shape of the Pentagon building.

• Hexagon (6 sides): Commonly found in nature, like the cells in a honeycomb.

• Heptagon (7 sides): Less common than the previous examples.

• Octagon (8 sides): Famously the shape of a stop sign.

And the list continues indefinitely, with names like nonagon (9 sides), decagon (10 sides), and so on.

Regularity: When Polygons are Perfect

A regular polygon is a special type of polygon. It has the distinguishing feature that all its sides are of equal length, and all its interior angles are equal in measure.

A square is a perfect example of a regular quadrilateral, while an equilateral triangle is a regular triangle. These perfectly symmetrical shapes hold a special place in geometry.

Chasing Infinity: Approaching the Infinite-Sided Polygon

Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments. Think of a humble triangle, a steadfast square, or even the more elaborate architecture of a hexagon. Each is a polygon, defined by a finite number of sides.

But what happens when we start to push the boundaries? What happens when we chase the elusive concept of infinity, applying it to these very polygons we've come to understand so well?

The Unbound Concept of Infinity

Infinity is one of those concepts that dances tantalizingly at the edge of our understanding. It's not a number in the traditional sense, but rather a concept representing something without any bound or limit. It signifies endlessness, a quantity greater than any assignable number.

In mathematics, infinity is often represented by the symbol ∞, the lemniscate, a sideways figure eight. It is a tool that allows us to discuss concepts and processes that continue without end.

Polygonal Growth: Towards the Limit

Now, imagine a polygon. Let's start with a simple square. Then, envision adding more and more sides: a pentagon, a hexagon, an octagon.

As the number of sides increases, something fascinating occurs: the shape begins to morph. It becomes smoother, its angles become more subtle, and its overall appearance begins to subtly change.

It looks increasingly less like a jagged polygon and more like a familiar, graceful circle.

The Circle as a Limit: A Glimpse into Calculus

Here's where the magic of calculus, specifically the concept of a limit, comes into play. In calculus, a limit is the value that a function "approaches" as the input gets closer and closer to some value.

Think of it like this: imagine a runner approaching a finish line. The runner gets closer and closer, but never actually touches the finish line. The finish line is the "limit" of the runner's progress.

Similarly, as the number of sides of our polygon approaches infinity, the polygon approaches a circle. This does not mean that a polygon with an infinite number of sides is a circle.

Instead, it means that the properties of the polygon (its area, its perimeter) get arbitrarily close to the properties of a circle. This is a subtle but crucial distinction.

The polygon never quite becomes a circle. It merely approaches it, forever chasing that perfect, curved form, illustrating the power of limits in mathematics.

The Circle: The Ultimate Polygon?

Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments. Now, let’s stretch our geometrical imagination. Can a circle, that most elegant of curves, also be considered a polygon? It's a bold question, but one that reveals a fascinating perspective on the nature of shapes and mathematical understanding.

Approaching Circularity: An Infinite Sum of Sides

The core argument rests on the idea that as the number of sides of a regular polygon increases without bound, the polygon's shape begins to resemble a circle more and more closely. Imagine a square morphing into an octagon, then a hexadecagon (16 sides), and so on. Each step brings us closer to perfect circularity.

The leap of intuition comes when we envision this process continuing indefinitely. The polygon, in this conceptualization, possesses an infinite number of sides.

Each side, consequently, would be infinitesimally small, approaching a length of zero. The jagged edges smooth out, eventually disappearing entirely to form the continuous curve we know as a circle.

Infinitesimal Sides: Building Blocks of Curvature

This idea of infinitesimally small sides is crucial. It provides a way to conceptualize the circle not as a fundamentally different entity from polygons, but rather as the ultimate polygon: a shape where the discrete nature of straight lines blurs into seamless curvature.

Think of it like pixels on a screen. When there are few pixels, the image looks blocky and jagged. But as the number of pixels increases, the image appears smoother and more realistic. In a circle, the "pixels" are infinite!

Relating Properties: From Polygon to Circle

If we accept this premise, the properties of polygons should translate to the circle as well. The perimeter of a polygon, the sum of all its sides, becomes the circumference of the circle. As the sides become infinitely small, the perimeter smoothly converges on this value.

Similarly, the area enclosed by the polygon approaches the area of the circle. We can use the polygon's area formula, manipulating it to account for the infinite sides to derive the area formula for a circle (πr²). This relationship reveals the deep connection between these shapes.

A Useful Model: Approximations in Action

It's important to acknowledge that this idea, while conceptually powerful, isn't a formal definition universally adopted in all areas of geometry. Rigorous mathematical proofs often rely on other approaches to define circles.

However, the notion of a circle as an infinite-sided polygon is an invaluable mental model.

It's a helpful tool for visualization and intuitive understanding.

It reinforces the idea that mathematical shapes are often connected in surprising and profound ways. It gives a practical route for approximating circles when exact constructions are not feasible. In many areas of practical mathematics, from computer graphics to engineering design, circles are frequently approximated by polygons with a very large number of sides, leveraging the concepts explained above.

Final Thoughts: Perspective and Understanding

Thinking of a circle as the ultimate polygon allows us to bridge the gap between the discrete world of polygons and the continuous elegance of curves. It fosters a deeper appreciation for mathematical connections and the power of conceptual models. While not a strictly formal definition, it's a rich and insightful way to understand the beauty and interconnectedness of mathematical shapes.

The Apeirogon: A Polygon of Countable Infinity

The Circle: The Ultimate Polygon? Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments. Now, let’s stretch our geometrical imagination. Can a circle, that most elegant of curves, also be considered a polygon? It's a bold question, but one that leads us to an even stranger, more abstract notion: the apeirogon.

But what lies beyond even the idea of a polygon with an infinite number of sides tending towards a circle? We delve into the realm of mathematical abstraction to encounter the apeirogon.

Defining the Apeirogon

An apeirogon, quite simply, is a polygon with a countably infinite number of sides and vertices. It’s a concept that pushes the boundaries of what we typically consider a polygon. Imagine a shape that extends infinitely in both directions, comprised of an endless sequence of line segments.

This isn't just about adding more and more sides to a regular polygon. It’s a leap into a different kind of infinity.

Abstraction Beyond the Circle

It's crucial to understand that the apeirogon is more abstract than the idea of a polygon with an increasing number of sides approaching a circle. The circle, in that context, is a limit. A shape we can conceptually grasp as the end result of a process.

The apeirogon, however, is infinite from the outset. It doesn’t "approach" anything; it is an infinite structure.

The Role of Countable Infinity

The term "countably infinite" is significant here. It means that while the number of sides and vertices is infinite, we can still establish a one-to-one correspondence between them and the set of natural numbers (1, 2, 3, ...).

This distinguish it from the "uncountable infinity" found in the real numbers.

Applications and Theoretical Relevance

While the apeirogon might seem purely theoretical, it finds applications in specific areas of mathematics. Discrete geometry, for instance, explores the properties of discrete shapes and structures, and the apeirogon can serve as a foundational element in certain models.

It also serves as a valuable theoretical construct for understanding limits and infinite processes.

A Mathematical Abstraction

Ultimately, the apeirogon exists as a mathematical abstraction. We cannot physically construct it or even accurately visualize it in its entirety. It’s a concept, a tool for exploring the boundaries of geometric definitions and pushing the limits of our mathematical understanding.

Apeirogon: An Infinite Line

A regular apeirogon would appear to be a straight line, extending infinitely in both directions.

This raises interesting questions about how we define shape and enclosure in an infinite context. A regular apeirogon's vertices all lie on a line, each spaced equally apart. A regular apeirogon can be seen as approaching a line as the number of sides go to infinity.

Mathematical Tools: Approximation and Geometric Understanding

The Apeirogon: A Polygon of Countable Infinity The Circle: The Ultimate Polygon? Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments. Now, let’s stretch our geometrical imagination. Can a circle, that most elegant of curves, also be considered a polygon? It might seem paradoxical, but as we explore the tools of approximation and geometric understanding, a fascinating connection emerges.

Polygons as Proxies: Approximating the Circle

The beauty of mathematics lies in its ability to provide incredibly accurate models of real-world phenomena. When it comes to shapes, polygons offer a powerful means of approximating curves, most notably the circle.

Imagine a square inscribed within a circle. Not a great fit, is it? Now, picture an octagon, then a hexadecagon (16 sides), and so on.

As the number of sides increases, the polygon hugs the circle more and more closely. This is no mere visual trick; it's a fundamental principle.

The greater the number of sides, the smaller the discrepancy between the polygon’s perimeter and the circle's circumference, and between the polygon’s area and the circle’s area. In essence, we’re replacing the smooth curve with a series of tiny, straight lines.

Practical Applications: Where Approximation Shines

This isn't just an abstract exercise. This principle of polygonal approximation fuels many technologies and calculations we rely on daily.

Computer Graphics

Consider computer graphics. Whether it's rendering a 3D sphere in a video game or creating a smooth curve in a design program, the underlying process often involves representing these shapes using polygons.

The more polygons used, the smoother and more realistic the final image appears. Zoom in close enough, and you'll see the individual polygons that make up the illusion of a curved surface.

Calculating Pi

The approximation technique even reaches into the very heart of mathematics by estimating the value of π (pi).

Ancient mathematicians used polygons inscribed and circumscribed within circles to determine increasingly accurate bounds for π. By calculating the perimeters of these polygons, they gradually narrowed down the possible values of π, getting closer and closer to its true value.

This elegant method underscores the relationship between polygons, circles, and one of the most fundamental constants in mathematics.

Geometry: The Framework for Understanding

Geometry provides the essential framework for understanding these relationships. It furnishes us with the tools to analyze shapes, measure distances and angles, and reason about spatial relationships.

It allows us to rigorously define concepts like "area," "perimeter," and "tangent," which are crucial for understanding both polygons and circles.

Geometry allows us to conceptualize and manipulate these figures in our minds, building a stronger grasp of how they relate to each other. It is the language in which we discuss the nature of space and shape.

Furthermore, it provides the rigor needed to formalize the notion of infinity in the context of geometric figures. This is how geometry bridges the gap between the finite and the infinite. By providing the tools and language to understand these concepts, it creates a profound connection between the abstract world of mathematics and our physical experiences.

The Nature of Definition: A Philosophical Perspective

Geometry, at its heart, is about shapes. Among the most fundamental of these are polygons: those closed, two-dimensional figures formed by straight line segments. Now, let’s stretch our geometrical imaginations and consider the philosophical implications of what happens when we push the boundaries of these definitions, especially as we approach the elusive concept of infinity.

The Shifting Sands of Mathematical Meaning

Extending the definition of a polygon to encompass shapes with an infinite number of sides is not merely a mathematical exercise.

It's a philosophical leap that forces us to confront the very nature of definition itself.

Is a circle truly an infinite-sided polygon, or is it something fundamentally different?

This question invites us to examine how mathematical definitions evolve and adapt to new concepts.

Mathematics is not a static body of knowledge; it's a living, breathing discipline where definitions are refined and expanded to accommodate new discoveries and insights.

When Does a Polygon Cease to Be?

Perhaps the most intriguing question is: at what point does a polygon transform into something else entirely?

Does it morph into a circle, an apeirogon, or simply an abstract mathematical idea?

This isn't a question with a definitive "yes" or "no" answer.

Instead, it compels us to consider the thresholds of definition and the subtle nuances that distinguish one mathematical object from another.

The act of naming gives identity; defining is about identity.

Definitions as Tools: Context is King

Ultimately, definitions are tools. Their usefulness hinges on the specific context in which they are applied.

A definition that works perfectly well in one area of mathematics might be inadequate or even misleading in another.

Consider the difference between the practical application of approximating a circle with a many-sided polygon (e.g., in computer graphics) and the theoretical consideration of an apeirogon in advanced geometry.

Each context demands a different level of precision and a different way of understanding the relationship between polygons and infinity.

The power of a definition, then, lies in its ability to serve a purpose – to illuminate, to clarify, and to advance our understanding of the mathematical world.

Definitions are not a fixed absolute, but instead are tools for navigation.

Video: What Shape Has the Most Sides? Infinity & Beyond!

Play Video

So, the next time you're drawing shapes, remember that while a googolgon has a lot of sides, the shape with the most sides is actually infinity and beyond! It's a wild concept, but hopefully, this article has helped you wrap your head around it. Now, go forth and contemplate the infinite possibilities of shapes!