Same Side Exterior Angles: Definition & Examples

Same side exterior angles, a geometric relationship, often pose a challenge in understanding transversal lines intersecting parallel lines, a concept extensively covered in Euclidean geometry textbooks and taught across educational institutions like Khan Academy. Transversal lines, acting as a tool, cut across two or more lines, creating various angle pairs, including the often misunderstood same side exterior angles. The properties of same side exterior angles are essential in proving lines are parallel, a theorem attributed to mathematicians throughout history.

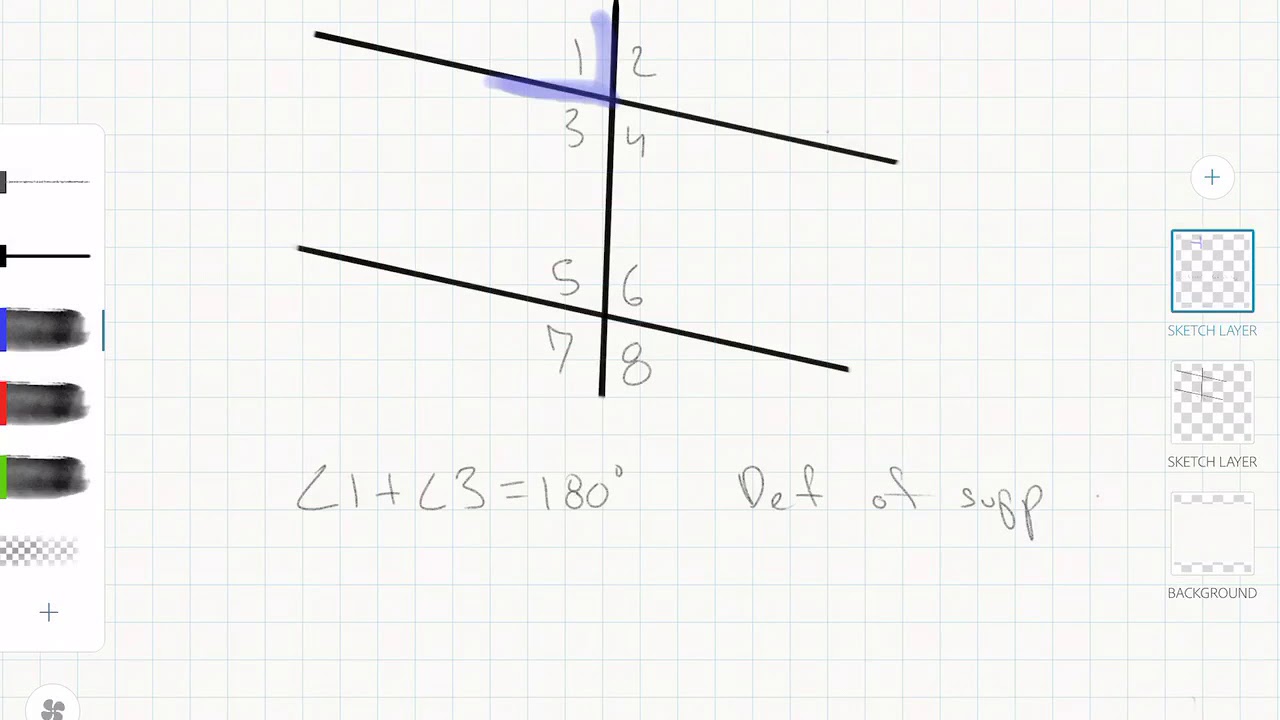
Image taken from the YouTube channel Paul Garrison , from the video titled Same side exterior angles .

Same side exterior angles are a fundamental concept in Euclidean geometry. They are formed when a transversal intersects two lines, creating a specific relationship between angles that lie outside the two lines and on the same side of the transversal. Understanding this relationship is crucial for grasping geometric proofs and spatial reasoning.

Definition of Exterior Angles

When a transversal intersects two lines, it creates eight angles. Exterior angles are those that lie outside the region between the two lines. In simpler terms, they are the angles that are not trapped between the two lines.

Consider two lines, line m and line n, intersected by a transversal t. The angles formed outside the space between lines m and n are considered exterior angles. It's important to visually identify these exterior angles before attempting to understand their relationships.

Defining "Same Side" in Relation to the Transversal

The term "same side" refers to the position of the exterior angles relative to the transversal. Imagine the transversal as a dividing line. Exterior angles that are on the same side of this transversal are considered "same side" exterior angles.

For example, if the transversal is leaning left-to-right, the exterior angles on the left side of the transversal are one set of same side exterior angles, and those on the right side form another set. Clarity in identifying which angles are on the same side is critical to applying the relevant theorems.

Importance in Euclidean Geometry

Same side exterior angles play a vital role in understanding fundamental geometric principles. They are particularly useful in determining whether two lines are parallel.

The key relationship to remember is that when parallel lines are cut by a transversal, same side exterior angles are supplementary, meaning they add up to 180 degrees. This property provides a powerful tool for analyzing geometric shapes and relationships.

Application in Geometry Proofs

One of the most significant applications of same side exterior angles is in geometric proofs. The supplementary relationship between same side exterior angles can be used as a basis for proving that two lines are parallel.

Conversely, if two lines are known to be parallel, the supplementary relationship can be used to deduce the measures of unknown angles. This logical connection is essential for constructing and understanding geometric arguments.

By understanding the definition, properties, and applications of same side exterior angles, you can enhance your geometric reasoning skills and build a strong foundation for more advanced concepts.

Foundational Geometric Concepts: Building Blocks

Before delving into the specifics of same side exterior angles, it's essential to establish a firm understanding of the underlying geometric principles. This section serves as a review of the core concepts that form the foundation for comprehending the relationships and properties of these angles. We'll cover the definition and measurement of angles, the nature of parallel lines and transversals, and a brief overview of other angle pairs that arise when a transversal intersects two lines.

The Role of Angles

Angles are fundamental to geometry. They dictate shapes, relationships, and measurements. Understanding their definition and how they are measured is crucial.

Definition and Measurement of Angles

An angle is formed by two rays (or line segments) that share a common endpoint, called the vertex. Angles are typically measured in degrees, with a full circle comprising 360 degrees. Radians are another unit of angular measure, often used in more advanced mathematical contexts.

There are various types of angles, including:

• Acute angles: Less than 90 degrees
• Right angles: Exactly 90 degrees
• Obtuse angles: Greater than 90 degrees but less than 180 degrees
• Straight angles: Exactly 180 degrees
• Reflex angles: Greater than 180 degrees but less than 360 degrees.

The type of angle influences its geometric properties and its relationships to other angles.

Use of a Protractor to Measure Angles

A protractor is the primary tool used to measure angles. To use a protractor, align its base with one ray of the angle, ensuring the vertex of the angle is at the center point of the protractor. The measure of the angle is then read from the scale where the other ray intersects the protractor.

Careful alignment and precise reading are necessary for accurate angle measurement.

Parallel Lines and the Transversal

Parallel lines and transversals create the necessary framework for exploring angle relationships.

Definition of Parallel Lines

Parallel lines are lines in a plane that never intersect. They maintain a constant distance from each other. A key property of parallel lines is that they have the same slope, if represented on a coordinate plane. The parallel postulate in Euclidean geometry states that, given a line and a point not on the line, there is exactly one line through the point that is parallel to the given line.

Parallel lines are fundamental to understanding angle relationships.

Explanation of the Transversal's Intersection

A transversal is a line that intersects two or more other lines. When a transversal intersects two lines, it creates several angles at the points of intersection. These angles form various pairs with specific relationships to each other. The relationships between these angles are particularly important when the two lines intersected by the transversal are parallel.

Angle Pairs Formed by a Transversal

A transversal creates a variety of angle pairs. These pairs have defined relationships that dictate their properties.

Overview of Corresponding Angles, Alternate Interior Angles, and Alternate Exterior Angles

When a transversal intersects two lines, it forms several angle pairs that have specific names and properties. Understanding these angle pairs provides context for understanding same side exterior angles.

• Corresponding angles are angles that occupy the same relative position at each intersection. If the two lines are parallel, corresponding angles are congruent (equal in measure).
• Alternate interior angles are angles that lie on opposite sides of the transversal and between the two lines. If the two lines are parallel, alternate interior angles are congruent.
• Alternate exterior angles are angles that lie on opposite sides of the transversal and outside the two lines. If the two lines are parallel, alternate exterior angles are congruent.

Focus on Same Side Exterior Angles

While other angle pairs are important, our focus remains on same side exterior angles. These angles lie on the same side of the transversal and outside the two lines. When the two lines are parallel, same side exterior angles are supplementary, meaning their measures add up to 180 degrees. This relationship is crucial in determining whether lines are parallel and in solving geometric problems.

Theorems and Properties of Same Side Exterior Angles

Having established the foundational geometric concepts, we can now delve into the defining characteristic of same side exterior angles: their supplementary relationship when formed by a transversal intersecting parallel lines. This section will explore this core property, its underlying theorem, and its powerful connection to proving parallelism.

The Supplementary Angles Relationship

The key property of same side exterior angles lies in their relationship when the lines intersected by the transversal are parallel. In this specific scenario, these angles are always supplementary.

Theorem: Same Side Exterior Angles are Supplementary Angles when Parallel Lines are cut by a Transversal

This fundamental theorem is the cornerstone of understanding same side exterior angles. It states: if two parallel lines are cut by a transversal, then the same side exterior angles are supplementary. In simpler terms, the sum of the measures of the two same side exterior angles will always equal 180 degrees.

This relationship provides a powerful tool for determining angle measures and analyzing geometric figures. For instance, if you know the measure of one same side exterior angle, you can immediately determine the measure of the other by subtracting the known angle from 180 degrees.

The theorem hinges on the parallelism of the two lines. If the lines are not parallel, this supplementary relationship does not hold true.

Visualizing the Theorem

While the theorem can be stated mathematically, its essence is best grasped visually. Imagine two parallel lines cleanly sliced by a transversal. The resulting same side exterior angles appear, intuitively, to "fill" the space of a straight angle (180 degrees).

To enhance understanding, the use of geometry software is highly recommended. Such tools allow for dynamic manipulation of the lines and transversal, visually demonstrating how the angle measures change while maintaining their supplementary relationship, as long as the lines remain parallel.

Conditions for Parallelism: The Converse Theorem

The supplementary relationship of same side exterior angles not only applies when lines are parallel but also serves as a test for parallelism. This is embodied in the converse of the theorem.

If Same Side Exterior Angles are Supplementary, then the Lines are Parallel

The converse of the theorem states: if two lines are cut by a transversal and the same side exterior angles are supplementary, then the lines are parallel. This is an extremely useful tool in geometric proofs and constructions.

This converse is just as important as the original theorem. It allows us to prove that two lines are parallel simply by demonstrating that their same side exterior angles, formed by a transversal, add up to 180 degrees.

It's crucial to remember that both angles must be measured or determined, and their sum must be verified to be exactly 180 degrees to conclusively prove parallelism using this method.

Connection to Related Theorems

The relationship between same side exterior angles and parallelism is deeply intertwined with other fundamental postulates and theorems in Euclidean geometry. One notable connection is to the Parallel Postulate.

The Parallel Postulate essentially guarantees the existence and uniqueness of parallel lines given a point and a line. The theorem regarding same side exterior angles and its converse provide a practical method for verifying the conditions described by the Parallel Postulate.

Furthermore, the understanding of same side exterior angles also reinforces concepts like angle congruence and supplementary angles, which are prevalent in various other geometric theorems and proofs. Mastering this relationship strengthens one's grasp of the broader geometric landscape.

Practical Applications and Problem Solving with Same Side Exterior Angles

Having explored the theoretical underpinnings of same side exterior angles, particularly their supplementary relationship when formed by a transversal intersecting parallel lines, we now shift our focus to the practical realm. This section delves into how this knowledge translates into tangible problem-solving skills, encompassing both algebraic calculations and real-world applications.

Calculating Angle Measures: Unveiling the Unknown

One of the most direct applications of the same side exterior angles theorem lies in determining unknown angle measures. When parallel lines are cut by a transversal, and the measure of one same side exterior angle is known, the measure of its counterpart can be readily calculated due to their supplementary relationship. This involves leveraging algebraic equations to solve for the unknown angle, solidifying the link between geometry and algebra.

Using Algebraic Equations to Find Unknown Angle Measures

The supplementary nature of same side exterior angles provides a fertile ground for algebraic problem-solving. Since the sum of their measures is always 180 degrees, we can express this relationship as an equation. Let's denote the measure of one angle as x and the measure of its same side exterior angle as y. Then, the equation becomes: x + y = 180°

If the value of x is known, we can easily solve for y by subtracting x from 180 degrees: y = 180° - x. This simple yet powerful equation is the key to unlocking numerous geometric problems.

For example, consider two parallel lines cut by a transversal. One of the same side exterior angles measures 110 degrees. To find the measure of the other angle, we substitute the known value into our equation: 110° + y = 180°. Solving for y, we find that y = 70°. Therefore, the measure of the other same side exterior angle is 70 degrees.

Example Problems Involving Same Side Exterior Angles

To further illustrate the process, let's consider a few more examples:

• Example 1: Two parallel lines are intersected by a transversal. One same side exterior angle is represented by the expression (2x + 10) degrees, and the other is (3x - 20) degrees. Find the value of x and the measure of each angle.

  • Solution: We know that (2x + 10) + (3x - 20) = 180. Combining like terms, we get 5x - 10 = 180. Adding 10 to both sides gives 5x = 190. Dividing by 5, we find x = 38. Substituting x = 38 into the expressions for the angles, we get (238 + 10) = 86 degrees and (338 - 20) = 94 degrees.

• Example 2: In a diagram, two parallel lines are cut by a transversal. One same side exterior angle is twice the size of the other. Find the measure of both angles.

  • Solution: Let x be the measure of the smaller angle. Then, the larger angle is 2x. Since they are supplementary, x + 2x = 180. This simplifies to 3x = 180. Dividing by 3, we get x = 60. Therefore, the smaller angle is 60 degrees, and the larger angle is 2*60 = 120 degrees.

These examples demonstrate the versatility of using algebraic equations to solve for unknown angle measures when dealing with same side exterior angles. By mastering this technique, one can confidently tackle a wide range of geometric problems.

Problem Solving in Real-World Contexts: Geometry in Action

The applications of same side exterior angles extend far beyond theoretical exercises. These geometric principles play a crucial role in various real-world scenarios, particularly in fields like architecture and engineering. Understanding these angles can be instrumental in ensuring structural integrity, precise measurements, and aesthetically pleasing designs.

Application of Same Side Exterior Angles in Architecture and Engineering

In architecture, the concept of parallel lines and transversals, and consequently same side exterior angles, is fundamental to creating stable and visually appealing structures. When designing buildings, architects must ensure that walls are parallel and that rooflines are angled correctly to provide adequate support and proper drainage.

For example, consider the design of a bridge. The support beams often run parallel to each other, and the roadway acts as a transversal. The angles formed by these intersections directly impact the load distribution and structural stability of the bridge. By carefully calculating and controlling these angles, engineers can ensure the safety and longevity of the structure.

Similarly, in building construction, understanding same side exterior angles can be crucial for tasks such as framing walls and installing roofing. Precise angle measurements are necessary to ensure that the structure is square and plumb, preventing potential structural problems down the line.

Examples That Require Understanding of Supplementary Angles to Solve

Let's consider a practical example in architecture: designing a gable roof. A gable roof consists of two sloping sides that meet at a ridge. The angle of the roof is crucial for both aesthetic reasons and for managing snow and water runoff.

Imagine that an architect wants to design a gable roof with a specific angle of inclination on one side. They know that the rafters (the sloping beams that support the roof) must be parallel to each other. If they know the angle that one rafter makes with the horizontal (the ground), they can use the principles of same side exterior angles to determine the angle that the other rafter needs to make with the horizontal to ensure that the roof is symmetrical and structurally sound.

Another example arises in road construction. When designing intersections, engineers need to consider the angles at which roads intersect to ensure safe and efficient traffic flow. Understanding the relationship between same side exterior angles formed by intersecting roads can help engineers design intersections that minimize blind spots and maximize visibility for drivers.

These real-world examples underscore the practical relevance of same side exterior angles. By applying this knowledge, architects and engineers can create structures that are not only aesthetically pleasing but also safe, stable, and functional.

Proofs and Geometric Constructions Involving Same Side Exterior Angles

This section delves into the practical application of same side exterior angles within the realms of formal geometric proofs and precise geometric constructions. We will explore how the supplementary relationship between these angles, when formed by a transversal intersecting two lines, serves as a powerful tool for both proving lines are parallel and constructing parallel lines with specified angular relationships.

Geometry Proofs Involving Same Side Exterior Angles

Geometric proofs are the cornerstone of deductive reasoning in geometry. They provide a logical and rigorous method for establishing the truth of a statement based on previously accepted axioms, definitions, and theorems. Same side exterior angles play a crucial role in proving that two lines are parallel.

Step-by-Step Examples of Proving Lines are Parallel

The most common application involves demonstrating that if same side exterior angles are supplementary, then the lines intersected by the transversal are indeed parallel. A typical proof might proceed as follows:

1. Given: State the given information, including the fact that two same side exterior angles formed by a transversal measure x and y, and that x + y = 180°.

2. Definition of Supplementary Angles: Acknowledge that angles are supplementary if the sum of their measures is 180°.

3. Application of the Converse of the Same Side Exterior Angles Theorem: State that if two lines are cut by a transversal such that the same side exterior angles are supplementary, then the lines are parallel.

4. Conclusion: Conclude that the two lines are parallel based on the given information and the converse of the same side exterior angles theorem.

Utilizing the Supplementary Nature of Same Side Exterior Angles

The supplementary relationship is the linchpin of these proofs. It's important to emphasize the precise and logical application of this relationship.

The proof must clearly show that the given angles are explicitly stated to be supplementary or that this can be derived from other givens using established geometric principles. Without this explicit demonstration, the proof is incomplete.

Geometric Constructions Related to Parallel Lines and Transversals

Beyond theoretical proofs, the principles of same side exterior angles are also essential in geometric constructions. Using only a compass and straightedge, we can accurately construct parallel lines and control the angles formed by their intersection with a transversal.

Constructing Parallel Lines Using a Ruler and Compass

Constructing parallel lines with a compass and straightedge relies on the properties of congruent corresponding angles, alternate interior angles, or same side exterior angles.

Here's a common method leveraging same side exterior angles:

1. Draw a Line and a Transversal: Begin by drawing a straight line, l, and then draw a transversal, t, intersecting l at a point A.

2. Create an Angle: At point A, an angle is formed. Choose a point B on line l distinct from A.

3. Replicate the Angle: Construct a congruent angle on the same side of the transversal at a different point C on the transversal. This can be done using compass and straightedge techniques to transfer the angle measure.

4. Draw the Parallel Line: Draw a line, m, through point C that forms the constructed angle. Since the same side exterior angles are supplementary, lines l and m are parallel.

Creating Same Side Exterior Angles with Specific Measurements

Constructing same side exterior angles with predetermined measures builds upon the construction of parallel lines.

After constructing the parallel lines as described above, the focus shifts to measuring and adjusting the angle formed by the transversal. If, for example, you want one same side exterior angle to measure 60 degrees, you would construct the transversal such that it forms a 60-degree angle with one of the parallel lines. Consequently, the other same side exterior angle will measure 120 degrees, fulfilling the supplementary requirement.

This process requires careful use of a protractor (after the compass and straightedge construction) to verify and, if necessary, adjust the angle measurements until the desired values are achieved. The accuracy of the construction directly depends on the precision of the compass and straightedge work, as well as the careful measurement with a protractor.

Video: Same Side Exterior Angles: Definition & Examples

Play Video

So, there you have it! Hopefully, understanding same side exterior angles doesn't feel like trying to solve a Rubik's Cube blindfolded anymore. With a little practice, you'll be spotting these angle pairs everywhere – and maybe even impressing your friends with your newfound geometry knowledge!