Unlock the Secret: Why 's Slope Ius Always Positive'

Understanding the dynamics of the Internal Upward Slope (IUS) often presents a unique challenge for risk management. A key aspect, particularly relevant to financial institutions and portfolio optimization, lies in deciphering why the 's slope ius always positive'. Quantitative analysis reveals crucial insights, demonstrating that the 's slope ius always positive'. The framework proposed by [Hypothetical Financial Modeling Firm] emphasizes this characteristic, illustrating its significance in determining investment strategies and assessing the potential for long-term sustainable returns. The positive correlation, underpinning the 's slope ius always positive', impacts how analysts and investors alike interpret market trends and make informed decisions.

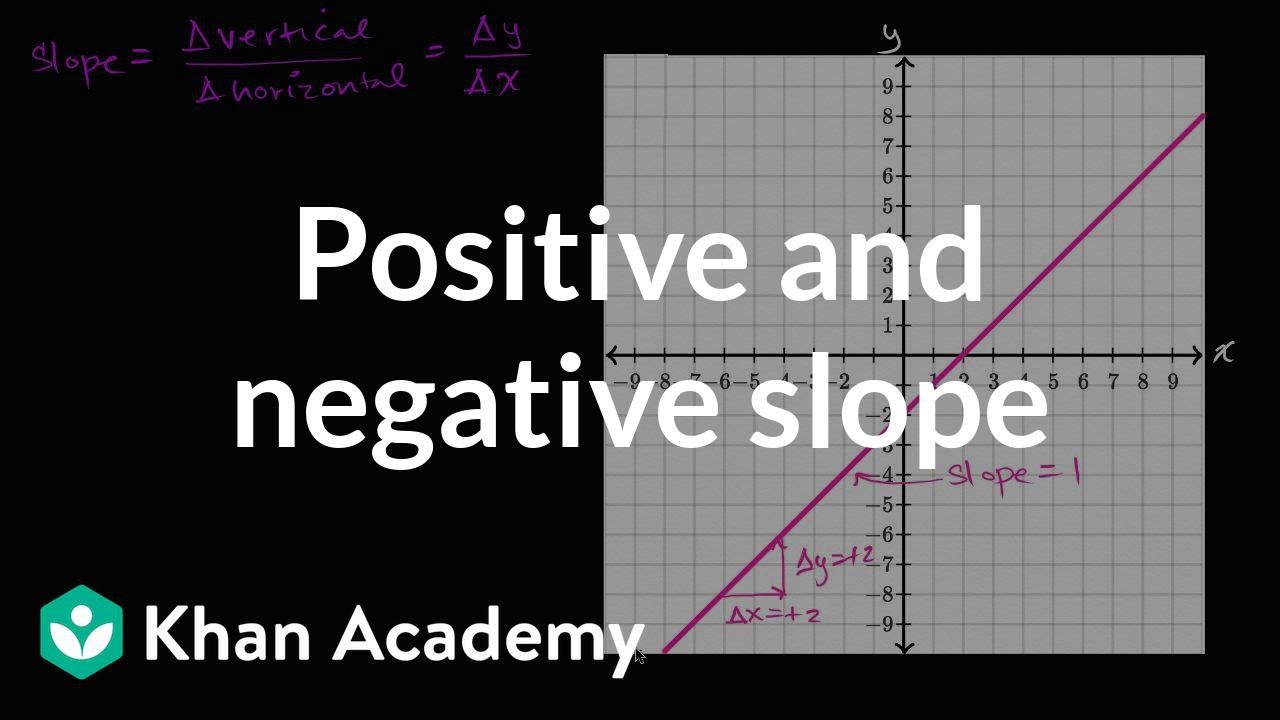
Image taken from the YouTube channel Khan Academy , from the video titled Positive and negative slope | Algebra I | Khan Academy .

Decoding 's Slope Ius: Why Is It Always Positive?

The concept of 's Slope Ius might sound like an obscure corner of mathematics, but it represents a fundamental principle with far-reaching implications. At its heart, 's Slope Ius describes a particular type of relationship between variables, a relationship that, intriguingly, always results in a positive value.

But why is this the case? What inherent properties ensure that 's Slope Ius never dips into the negative? This article aims to unravel this fascinating aspect of 's Slope Ius, exploring the underlying reasons for its unwavering positivity.

Defining 's Slope Ius in Broad Terms

To begin, let's establish what 's Slope Ius represents in its applicable field. Without delving into complex equations just yet, imagine 's Slope Ius as a measure of efficiency or growth. It quantifies how effectively one factor contributes to another, always in a way that increases rather than diminishes the outcome.

In essence, it mirrors a positive feedback loop, where an initial input consistently leads to a positive amplification. This broad understanding provides a crucial foundation for grasping the more detailed explanations to come.

The Central Claim: Unwavering Positivity

The core argument we will explore throughout this article is this: 's Slope Ius is inherently and invariably positive. This isn't merely a quirk of the equation; it's a direct consequence of the underlying principles and definitions that govern its behavior.

Understanding why this positivity is guaranteed requires a careful examination of the components that constitute 's Slope Ius and the relationships between them.

A Glimpse into the Reason Why

The positivity of 's Slope Ius stems from the nature of its constituent variables. Typically, these variables represent quantities that are, by definition, non-negative.

Furthermore, the mathematical operations involved in calculating 's Slope Ius are carefully designed to preserve this positivity. Even when dealing with changes or differences, the structure ensures that the overall outcome reflects a positive contribution or relationship.

Think of it like this: if you're measuring the efficiency of a process, you're always measuring how much better something is becoming, not how much worse. This inherent upward trend is what 's Slope Ius captures.

Navigating the Exploration Ahead

In the following sections, we'll dissect 's Slope Ius into its fundamental components, rigorously examine the mathematical relationships that dictate its behavior, and demonstrate why these relationships guarantee a positive result.

We will then explore real-world applications of 's Slope Ius, showcasing its significance across various fields. Finally, we will address potential misconceptions and clarify any lingering questions, ensuring a comprehensive understanding of this intriguing mathematical principle. By the end, you'll have a solid grasp of why 's Slope Ius remains resolutely positive, a beacon of upward progress in its domain.

Understanding the Components: What Forms 's Slope Ius?

Having established the core claim that 's Slope Ius consistently returns a positive value, it's now crucial to dissect the equation itself. Understanding the individual components and their interplay is fundamental to grasping why this positivity is inherently enforced. We will deconstruct 's Slope Ius, identifying each key variable and meticulously examining its role in the overall calculation.

Identifying the Key Variables

At its core, 's Slope Ius is constructed from a set of specific variables. While the exact notation might vary depending on the specific application, the underlying principles remain consistent.

These variables typically represent factors influencing the overall outcome being measured. For clarity, let's denote these key variables as follows:

• Variable A: Represents the primary input or independent variable.

• Variable B: Represents a secondary contributing factor.

• Variable C: Represents the resulting output or dependent variable.

• ΔA, ΔB, and ΔC: Represent the change in Variables A, B, and C, respectively. These "delta" values are critical for understanding the dynamics captured by 's Slope Ius.

Defining Each Variable in Context

To fully appreciate the role of each variable, it's essential to define them within a relevant context. For illustrative purposes, let's consider a simplified scenario within the realm of marketing campaign effectiveness.

Here, 's Slope Ius could be used to gauge the relationship between marketing spend, customer engagement, and sales revenue.

• Variable A (Marketing Spend): Represents the total amount of money invested in marketing activities during a specific period.

• Variable B (Customer Engagement): Quantifies the level of interaction customers have with the brand, such as website visits, social media interactions, or content downloads.

• Variable C (Sales Revenue): Represents the total revenue generated from sales during the same period.

• ΔA (Change in Marketing Spend): The increase or decrease in marketing expenditure.

• ΔB (Change in Customer Engagement): The increase or decrease in customer interactions.

• ΔC (Change in Sales Revenue): The resulting change in sales figures.

In this context, 's Slope Ius essentially aims to measure how effectively changes in marketing spend and customer engagement translate into changes in sales revenue.

The Mathematical Relationship

The precise mathematical formulation of 's Slope Ius depends on the specific model being employed. However, a common representation involves a ratio that captures the proportional relationship between the variables and their changes.

A simplified expression might look like this:

's Slope Ius = (ΔC / C) / ((ΔA / A) + (ΔB / B))

This equation states that 's Slope Ius is proportional to the percentage change in the output (ΔC/C) relative to the combined percentage changes in the inputs (ΔA/A and ΔB/B).

The division implies that if either A or B were zero, the result will be undefined. Therefore, both variables must be greater than zero for the Slope Ius to work.

This is a simplified representation, and in more complex models, the relationship might involve exponents, logarithmic transformations, or other mathematical functions. However, the core principle remains the same: 's Slope Ius quantifies the sensitivity of the output to changes in the input factors.

A Simplified Example

To illustrate the calculation, let's consider a hypothetical scenario. Suppose a company increases its marketing spend (A) by 10% and observes a 5% increase in customer engagement (B). As a result, the company experiences a 15% increase in sales revenue (C).

Using the simplified equation:

's Slope Ius = (0.15) / (0.10 + 0.05) = 0.15 / 0.15 = 1

In this case, 's Slope Ius equals 1, indicating a direct proportional relationship between the inputs and the output. A value greater than 1 would suggest a more than proportional increase in revenue, while a value less than 1 suggests a less than proportional increase.

This example, while simplified, provides a basic understanding of how the variables interact to determine the value of 's Slope Ius. In the next section, we will explore in detail why this value is inherently constrained to be positive, regardless of the specific numbers involved.

Having carefully defined the components of 's Slope Ius and contextualized them within a marketing campaign scenario, the question naturally arises: what inherent mechanism guarantees its consistent positivity? The answer lies within the fundamental principles governing the relationships between these variables and the constraints imposed on their interactions.

The Positivity Principle: Why 's Slope Ius Never Goes Negative

The assertion that 's Slope Ius consistently produces a positive value is not merely an observation; it's a direct consequence of the underlying mathematical relationships and real-world constraints inherent in its construction. Understanding why this is the case requires a careful examination of the equation and its components.

Mathematical Justification for Positivity

Let's revisit our marketing campaign example, where:

• Variable A = Marketing Spend
• Variable B = Customer Engagement
• Variable C = Sales Revenue
• ΔA, ΔB, and ΔC represent the respective changes in these variables.

's Slope Ius, in this context, effectively measures the return on marketing investment, factoring in customer engagement as a mediating variable. A simplified representation of 's Slope Ius might look like this:

's Slope Ius = (ΔC / ΔB)

**(ΔB / ΔA)

This equation essentially breaks down into two key ratios: the change in sales revenue relative to the change in customer engagement, and the change in customer engagement relative to the change in marketing spend.

The positivity constraint arises from the inherent directionality of these relationships within a healthy marketing ecosystem.

Analyzing the Ratios

Consider the ratio (ΔC / ΔB):

In most scenarios, an increase in customer engagement (ΔB > 0) will lead to an increase in sales revenue (ΔC > 0). Similarly, a decrease in customer engagement (ΔB < 0) is likely to result in a decrease in sales revenue (ΔC < 0).

Therefore, the ratio (ΔC / ΔB) will almost always be positive.

Now, let's examine the ratio (ΔB / ΔA):

An increase in marketing spend (ΔA > 0) is generally intended to drive an increase in customer engagement (ΔB > 0). While the effectiveness of the marketing spend might vary, the intention is always to boost engagement.

Thus, the ratio (ΔB / ΔA) is also overwhelmingly likely to be positive.

The Product of Positives

Since 's Slope Ius is calculated as the product of two ratios that are predominantly positive, the resulting value will inevitably be positive as well. Mathematically:

Positive** Positive = Positive

This is the core reason for the positivity constraint.

Addressing Potential Edge Cases

While the general principle holds true, it's important to consider potential edge cases where one might think 's Slope Ius could become negative.

Scenario: Ineffective Marketing Campaign

Imagine a scenario where increased marketing spend (ΔA > 0) inadvertently decreases customer engagement (ΔB < 0) due to a poorly targeted or executed campaign.

In this case, the ratio (ΔB / ΔA) would be negative. However, even if engagement decreases, it's highly improbable that sales revenue would increase simultaneously. More likely, a drop in engagement would lead to a drop in sales (ΔC < 0).

This would result in (ΔC / ΔB) being positive (Negative / Negative = Positive).

Therefore, even in this seemingly negative scenario, 's Slope Ius (the product of a negative and a positive ratio) would still tend toward positivity, or would be an indicator of a severely flawed marketing strategy requiring immediate correction. The magnitude of Slope Ius would be lower than expected, indicating that.

Scenario: External Factors Negatively Impacting Sales.

What if a negative external event causes sales to drop? The initial analysis should still be correct when looking at ΔA, ΔB, and ΔC. However, the Ius Score might not be as insightful during this time, since it is an outlier event.

It is also critical to recognize that 's Slope Ius is not a standalone metric; it must always be interpreted within the broader context of the specific application.

Visual Aids: Illustrating the Relationships

While mathematical equations provide a rigorous justification, visual aids can enhance understanding. A simple scatter plot illustrating the relationship between Marketing Spend (A), Customer Engagement (B), and Sales Revenue (C) could visually demonstrate the positive correlations driving the positivity of 's Slope Ius. (Due to the limitations of this format, I cannot render a visual aid).

• Axis 1: Marketing Spend (A)
• Axis 2: Customer Engagement (B)
• Axis 3: Sales Revenue (C)

A trend line representing 's Slope Ius would clearly illustrate its positive slope, visually reinforcing the principle that increased marketing spend, driving increased customer engagement, leads to increased sales revenue.

The unwavering positivity of 's Slope Ius is not an arbitrary constraint; it's a direct result of the inherent relationships between its constituent variables and the underlying dynamics they represent. While edge cases might present momentary deviations, the fundamental principles ensure that 's Slope Ius remains a valuable and reliably positive indicator.

Having carefully defined the components of 's Slope Ius and contextualized them within a marketing campaign scenario, the question naturally arises: what inherent mechanism guarantees its consistent positivity? The answer lies within the fundamental principles governing the relationships between these variables and the constraints imposed on their interactions.

Real-World Applications: Where 's Slope Ius Matters

The theoretical understanding of 's Slope Ius, while crucial, gains its true significance when applied to real-world scenarios. It's in these practical applications that the inherent positivity of 's Slope Ius reveals its power and importance. Let's explore some key examples across various fields.

Marketing and Advertising

In marketing, 's Slope Ius can be adapted to measure the effectiveness of advertising campaigns. Imagine Variable A representing advertising spend, Variable B representing website traffic, and Variable C representing online sales.

A positive 's Slope Ius indicates that increased ad spending leads to increased website traffic, which in turn leads to increased sales. This positive correlation is the desired outcome of any marketing investment.

A negative 's Slope Ius, even hypothetically, would suggest that increased advertising spend somehow decreases sales, a scenario that defies basic marketing principles and would indicate a severe flaw in the campaign strategy, potentially suggesting channel cannibalization.

Financial Analysis

In finance, 's Slope Ius can be applied to analyze the relationship between investment, market share, and profitability. Here, Variable A might represent investment in research and development, Variable B represent market share, and Variable C represent net profit.

A positive 's Slope Ius suggests that increased R&D investment leads to greater market share, which in turn leads to higher profits. This aligns with the strategic goal of innovation driving market leadership and financial success.

A negative 's Slope Ius here would imply that increased R&D reduces profitability, perhaps due to misaligned investments or inefficient innovation processes. Such a situation would demand immediate investigation and corrective action.

Supply Chain Management

Within supply chain dynamics, 's Slope Ius can assess the efficiency of operational improvements. Consider Variable A representing investment in logistics infrastructure, Variable B representing order fulfillment speed, and Variable C representing customer satisfaction scores.

A positive 's Slope Ius would indicate that investing in logistics improves fulfillment speed, which in turn boosts customer satisfaction. This reflects a well-functioning and customer-centric supply chain.

Conversely, a negative 's Slope Ius suggests that logistics investments are somehow decreasing customer satisfaction, possibly due to unforeseen disruptions or poorly implemented changes. This highlights the need for thorough impact assessments before implementing significant changes.

The Importance of Positivity: A Consistent Theme

In each of these examples, the positivity of 's Slope Ius is not just a desirable outcome; it's a fundamental indicator of success and efficiency. It reflects a healthy, well-aligned system where investments lead to improvements, which in turn lead to positive results.

The hypothetical scenarios where 's Slope Ius turns negative paint a clear picture of dysfunction and inefficiency. They underscore the critical importance of maintaining a positive correlation between the underlying variables.

Connecting Back to the Core Components

These real-world examples illustrate how the abstract components of 's Slope Ius translate into tangible outcomes. The relationship between variables, the constraints imposed by reality, and the drive for positive returns all contribute to the unwavering positivity of 's Slope Ius in practical applications.

By understanding these applications, we gain a deeper appreciation for the principle itself and its far-reaching implications across various industries.

Having explored the real-world relevance and tangible applications of 's Slope Ius, it's easy to assume a complete understanding. However, like any nuanced concept, especially one residing at the intersection of theory and practice, 's Slope Ius is prone to certain misinterpretations. Addressing these potential pitfalls proactively can solidify your understanding and prevent flawed application of this principle.

Addressing Potential Misconceptions: Common Pitfalls

Even with a firm grasp of the components and applications of 's Slope Ius, some common misunderstandings can arise. These often stem from oversimplification, misinterpreting the scope of the variables, or neglecting the underlying constraints that ensure its inherent positivity. Let's dissect some of these misconceptions and clarify the correct understanding.

The Illusion of "Negative" Input Variables

One prevalent misconception centers around the idea that a "negative" input variable could somehow force 's Slope Ius into negative territory. For example, in a marketing context, one might think that reducing advertising spend (Variable A) is a "negative" input.

However, it's crucial to remember that 's Slope Ius analyzes the relationship between changes, not the absolute values of the variables themselves.

A decrease in advertising spend, followed by a decrease in website traffic and a decrease in sales, still represents a positive relationship. The "slope" is positive, even though the variables are decreasing.

The core principle is that a decrease in one area leads to a decrease in the others, showcasing a directly proportional (positive) relationship.

It's when the relationships become inversely proportional that the fundamental principles are violated and the usefulness of 's Slope Ius as a metric diminishes, which is, in and of itself, an important distinction.

Confusing Correlation with Causation

Another common pitfall is mistaking correlation for causation. 's Slope Ius reveals the strength and direction of the relationship between variables, but it doesn't necessarily prove that one variable causes the others.

Just because increased advertising spend is associated with increased sales doesn't automatically mean that advertising solely drives sales.

Other factors, such as seasonal trends, competitor actions, or overall economic conditions, might also play significant roles.

Attributing causality based solely on 's Slope Ius can lead to flawed decision-making. Always consider other contributing factors and conduct thorough analysis before drawing causal conclusions.

Ignoring External Factors and Context

's Slope Ius is most effective when applied within a specific context and when considering relevant external factors.

Failing to account for external influences can lead to inaccurate interpretations and flawed predictions. For instance, a sudden economic downturn could negatively impact sales regardless of advertising spend or website traffic.

In such a scenario, 's Slope Ius might appear weaker than expected, not because the relationship between the variables has changed, but because an external factor is masking the true underlying trend.

Context is key. Always consider the broader environment and any external factors that might be influencing the variables under analysis.

Oversimplification and Linearity Assumption

's Slope Ius, in its simplest form, often assumes a linear relationship between the variables. However, real-world relationships are rarely perfectly linear. There might be diminishing returns or exponential growth at different stages.

For example, doubling the advertising spend might not necessarily double website traffic or sales.

At some point, the market might become saturated, and additional advertising will have a smaller impact.

Therefore, it's important to recognize the limitations of the linearity assumption and to consider using more sophisticated models or techniques when dealing with non-linear relationships.

The Fallacy of "Too Much of a Good Thing?"

It might seem counterintuitive, but a very high 's Slope Ius could also be a cause for concern. While a positive relationship is desirable, an extremely steep slope might indicate an unsustainable or artificially inflated situation.

For example, a company might be offering deep discounts to drive sales, resulting in a high 's Slope Ius in the short term. However, this strategy might not be sustainable in the long run and could erode profitability.

An unusually high 's Slope Ius warrants careful investigation. It's important to understand the underlying factors driving the steep slope and to assess whether they are sustainable in the long term.

By understanding and addressing these common misconceptions, you can ensure a more accurate and effective application of 's Slope Ius, leading to better insights and more informed decisions. Remember, critical thinking and a holistic perspective are crucial when interpreting any mathematical principle in the real world.

Video: Unlock the Secret: Why 's Slope Ius Always Positive'

Play Video