Are All Quadrilaterals Trapezoids? Geometry Truth

The world of Euclidean geometry, a cornerstone of mathematical understanding since Euclid's Elements, often presents concepts that seem straightforward but hide layers of complexity. Quadrilaterals, polygons defined by four sides, appear simple enough, yet their relationship to specific classifications such as trapezoids raises intriguing questions. The Trapezoid Song, with its catchy tune, might leave one thinking that all shapes fit neatly into predefined boxes, but are all quadrilaterals trapezoids? Geometry, much like the precise calculations performed at NASA's Jet Propulsion Laboratory (JPL) for spacecraft trajectories, demands accuracy and careful consideration of definitions, and exploring this question leads us down a fascinating path of mathematical exploration.

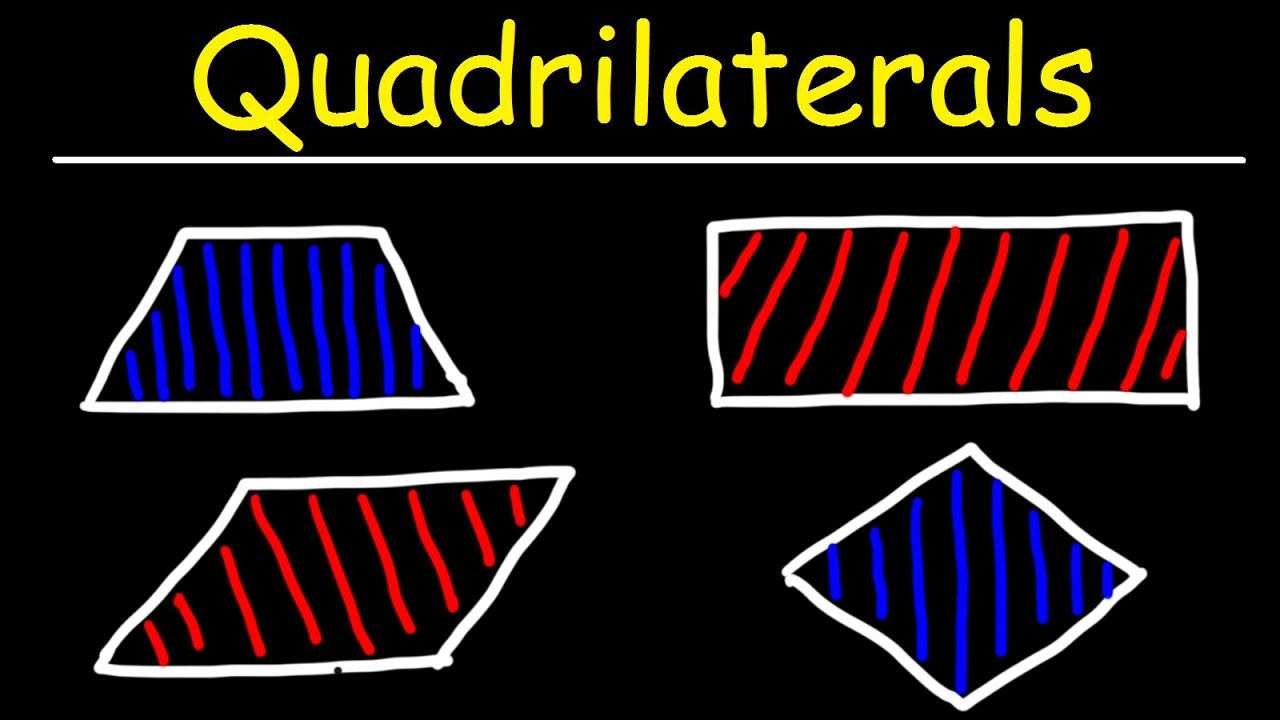
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Quadrilaterals - Trapezoids, Parallelograms, Rectangles, Squares, and Rhombuses! .

Unveiling the World of Quadrilaterals: A Geometric Odyssey

Geometry, the bedrock of spatial understanding, unveils the universe of shapes, sizes, and the intricate relationships they share. It's more than just lines and angles; it’s a lens through which we perceive and interpret the physical world.

The Foundation: Euclidean Geometry

Within this vast landscape of geometric principles, Euclidean Geometry stands as a monumental achievement. It’s the classical system, a rigorous framework, meticulously built upon axioms and postulates, providing the very foundation for our understanding of quadrilaterals. Every theorem, every definition regarding these fascinating shapes, traces its lineage back to Euclid's seminal work. It is the lens to view and classify quadrilaterals.

Setting the Course: Why Quadrilaterals Matter

But why focus on quadrilaterals? Why dedicate our attention to these four-sided figures?

The answer lies in their pervasive presence and fundamental role. This blog post embarks on a journey to explore the definitions, properties, and intricate relationships that define the quadrilateral family.

We aim to uncover their real-world significance, illustrating how these shapes, often taken for granted, are essential building blocks of our environment and crucial tools in various disciplines. Prepare to rediscover the quadrilateral, from its most basic form to its most elegant manifestation.

Defining the Basics: What is a Quadrilateral?

Having set the stage for our geometric exploration, we now turn our attention to the foundational element of our discussion: the quadrilateral itself. Before diving into the nuances of trapezoids and their relationship to other four-sided figures, we must first establish a clear and comprehensive understanding of what constitutes a quadrilateral.

The Essence of a Quadrilateral: A Four-Sided Foundation

At its core, a quadrilateral is defined as a polygon possessing four sides and, consequently, four angles. This simple definition serves as the bedrock upon which all subsequent classifications and properties are built. Think of it as the genetic code shared by all members of the quadrilateral family.

Quadrilateral: The Umbrella Term

It's crucial to recognize that 'quadrilateral' is the overarching category. It’s the wide-open field where squares, rectangles, parallelograms, and trapezoids all frolic. Understanding this hierarchical relationship is key to unraveling the apparent paradox of the question at hand: "Are all quadrilaterals trapezoids?"

Angles, Sides, and the Dance of Definition

The character of a quadrilateral is further defined by the interplay of its sides and angles. The lengths of the sides, whether they are equal or unequal, and the measures of the angles, whether they are right, acute, or obtuse, contribute to the unique identity of each quadrilateral.

Parallel Lines: A Defining Twist

The presence, absence, and arrangement of parallel lines become pivotal in classifying quadrilaterals into distinct subcategories, such as trapezoids and parallelograms, as we shall see. The arrangement and properties of parallel lines are the primary criteria for differentiation.

Sides as Boundaries: The Perimeter of Possibility

The sides of a quadrilateral are, in essence, line segments. These segments, when connected, form the closed boundary of the shape. They define its perimeter and contribute to its overall area.

They are the structural framework, the very lines that give a quadrilateral its tangible form and allow us to perceive it as a distinct geometric entity. Understanding the definition of a quadrilateral is a necessary preamble to exploring the nuances of the quadrilateral world.

Trapezoids and Trapeziums: The Foundation of the Hierarchy

Having established the fundamental definition of a quadrilateral, we now embark on a journey into the diverse world of specific quadrilateral types. Our exploration begins with the trapezoid (or trapezium, depending on your geographic location), a shape that holds a pivotal position in the quadrilateral hierarchy. It's a cornerstone of geometric understanding, serving as a gateway to more specialized forms.

Defining the Trapezoid: At Least One Pair of Parallel Lines

The defining characteristic of a trapezoid is elegant in its simplicity: it is a quadrilateral possessing at least one pair of parallel sides. This "at least" is a critical nuance. It's what separates the trapezoid from the parallelogram, and consequently, the other shapes further up the hierarchy.

These parallel sides are known as the bases of the trapezoid. The non-parallel sides are referred to as the legs. Understanding these terms is essential for navigating the landscape of trapezoid properties.

Properties of Trapezoids: A Symphony of Angles and Sides

While the presence of at least one pair of parallel sides defines the trapezoid, other properties contribute to its unique character. The angles formed by the bases and legs exhibit specific relationships.

Angle Relationships: Supplementary Pairs

Specifically, the angles on each of the non-parallel sides are supplementary, meaning they add up to 180 degrees. This supplementary relationship stems directly from the parallel postulate and the properties of parallel lines cut by a transversal.

Median Marvel: The Midsegment of a Trapezoid

Another noteworthy property is the midsegment (or median) of a trapezoid. This is the line segment connecting the midpoints of the non-parallel sides. The midsegment is parallel to the bases, and its length is equal to the average of the lengths of the bases.

Varieties of Trapezoids: Isosceles and Right-Angled

The trapezoid family isn't monolithic. There are different varieties of trapezoids, each with its own distinctive features.

Isosceles Trapezoids: Symmetry and Elegance

One prominent type is the isosceles trapezoid. In this variation, the non-parallel sides (legs) are of equal length. This equality leads to further symmetrical properties, such as equal base angles. Isosceles trapezoids possess a line of symmetry down the middle.

Right-Angled Trapezoids: A Touch of Orthogonality

Another type is the right-angled trapezoid, which features at least one right angle. This often arises when one of the non-parallel sides is perpendicular to the bases.

Understanding these specific types expands our comprehension of the trapezoid's versatility. Each type has unique applications in geometric problem-solving and design.

Trapezoids: More Than Just a Shape

The trapezoid serves as a foundational step in understanding the hierarchy of quadrilaterals.

By understanding its defining characteristic—the presence of at least one pair of parallel sides—and exploring its various properties and subtypes, we lay a solid groundwork for exploring more specialized quadrilaterals like parallelograms, rectangles, rhombuses, and squares. The trapezoid is more than just a shape; it's a key to unlocking the secrets of the quadrilateral family.

Parallelograms: Stepping Up the Parallel Game

Having journeyed through the world of trapezoids, where at least one pair of parallel sides reigns supreme, we now ascend to a higher echelon in the quadrilateral hierarchy: the parallelogram. Here, the game of parallelism intensifies, demanding two pairs of parallel lines. This seemingly simple condition unlocks a cascade of unique and elegant properties, transforming the shape and expanding its geometric possibilities.

Defining the Parallelogram: A Symphony of Parallelism

A parallelogram, at its core, is a quadrilateral. But it is no ordinary quadrilateral. It distinguishes itself by possessing two pairs of parallel sides. This is the defining characteristic, the key that unlocks all its other remarkable attributes.

Think of it as an evolved trapezoid, having achieved a higher level of symmetry and balance. The presence of two pairs of parallel lines creates a harmonious interplay between sides and angles, resulting in predictable and useful relationships.

Properties of Parallelograms: Unveiling the Geometric Harmony

The dual parallel nature of parallelograms gives rise to a beautiful suite of properties. These properties are not merely aesthetic; they are fundamental to solving geometric problems and understanding spatial relationships.

Opposite Sides and Angles: A Tale of Equality

Perhaps the most striking property of a parallelogram is the equality of its opposite sides. This means that not only are the opposite sides parallel, but they are also congruent, having the same length.

Similarly, opposite angles in a parallelogram are also equal. This creates a sense of balance and symmetry, making the shape visually pleasing and mathematically predictable. These relationships stem directly from the parallel postulates and transversal properties.

Diagonals: Bisecting the Balance

The diagonals of a parallelogram, those line segments connecting opposite vertices, also possess a special relationship. They bisect each other. This means they intersect at their midpoints, dividing each other into two equal segments.

This property is particularly useful in various geometric constructions and proofs. It allows us to establish relationships between different parts of the parallelogram and derive further conclusions.

The Parallelogram: A Cornerstone of Geometry

The parallelogram is far more than just a shape with two pairs of parallel lines. It is a fundamental building block in geometry. Its properties and relationships are essential for understanding more complex shapes and solving challenging geometric problems.

From architecture to engineering, the principles of parallelograms are applied in countless real-world applications. They provide a foundation for stability, balance, and structural integrity. Understanding the parallelogram unlocks a deeper appreciation for the elegance and power of geometry in our world.

Rectangles: The Right-Angled Parallelogram

Emerging from the world of parallelograms, we encounter a shape of particular elegance: the rectangle. The rectangle takes the inherent symmetry and balance of a parallelogram and elevates it through a single, defining addition: right angles. This seemingly small change has profound consequences, granting the rectangle properties that make it a cornerstone of both geometry and design.

Defining the Rectangle: A Parallelogram Perfected

At its heart, a rectangle is a parallelogram. That means it inherits all the properties of its parent shape. However, a rectangle distinguishes itself with a specific and crucial qualification: all four of its angles are right angles (90 degrees). This one attribute transforms a common parallelogram into a particularly useful and visually appealing shape.

Think of it as a parallelogram that has been "squared up." The angles, once potentially oblique, are now perfectly perpendicular. This angular perfection gives the rectangle its characteristic stability and predictable properties.

Properties of Rectangles: Inherited and Enhanced

Because a rectangle is a parallelogram, it automatically possesses certain attributes. These include having opposite sides that are parallel and congruent.

However, the presence of right angles enhances and adds to these properties. The most important consequence is the congruence of the diagonals.

Diagonals of a Rectangle: A Tale of Congruence

While the diagonals of a general parallelogram bisect each other, the diagonals of a rectangle are not just bisecting; they are also congruent. This means they have the same length.

This unique property arises directly from the presence of the right angles. The diagonals divide the rectangle into four triangles, and the right angles ensure that these triangles are related in a way that guarantees equal diagonal lengths.

Sides of a Rectangle: Equal, Parallel, and Predictable

In any rectangle, opposite sides are both parallel and congruent, as it inherits from being a parallelogram.

This simple characteristic leads to structural stability and straightforward calculations of area and perimeter. These easily calculated properties make the rectangle invaluable in design and engineering.

The Rectangle: A Foundation of Form and Function

The rectangle is more than just a shape with four right angles. It’s a fundamental building block in design, architecture, and many areas of mathematics and engineering.

Its easily understood properties and inherent stability make it an indispensable tool. The rectangle's presence is ubiquitous in the world around us, from the pages of books to the foundations of buildings. Truly, the rectangle is both beautiful and functionally versatile.

Rhombuses: Equality on All Sides

From the realm of parallelograms emerges another captivating shape: the rhombus. While parallelograms boast parallel opposite sides, the rhombus elevates this with a striking declaration of equality: all four sides are congruent. This simple yet profound addition unlocks a wealth of unique geometric properties, setting the rhombus apart as a figure of both beauty and utility.

Defining the Rhombus: A Parallelogram of Equals

At its core, a rhombus is a parallelogram. It inherits all the defining characteristics: two pairs of parallel sides, opposite angles that are equal, and diagonals that bisect each other. However, the rhombus distinguishes itself with a crucial constraint: all four sides are of equal length. This seemingly small requirement has substantial implications for the rhombus's angles, diagonals, and overall symmetry.

The rhombus presents a harmonious balance. It's a parallelogram that has embraced equality across all its sides, creating a unique and versatile geometric form.

Key Properties of the Rhombus: Unveiling the Consequences of Equality

The defining characteristic of the rhombus — four equal sides — has cascading effects, leading to a number of distinctive properties. These properties govern its angles, diagonals, and symmetry, making it a fascinating subject of geometric study.

Angles: Opposite and Equal

Like all parallelograms, a rhombus possesses opposite angles that are equal. This is a direct consequence of its parallel sides and inherent symmetry. However, the equality of the sides does not force the rhombus to have right angles; it can adopt any set of opposite angle pairs that add to 360 degrees.

Diagonals: Perpendicular Bisectors

Perhaps the most distinctive property of the rhombus lies in its diagonals. Not only do the diagonals bisect each other (as in all parallelograms), but they also intersect at right angles. This means the diagonals of a rhombus are perpendicular bisectors of each other.

This perpendicularity is directly linked to the equal side lengths. It forces a symmetry that demands the diagonals meet at a perfect 90-degree angle.

The diagonals divide the rhombus into four congruent right triangles, a fact that is invaluable when calculating area and solving geometric problems.

Rhombus in the Real World: Applications and Significance

The rhombus is more than just a geometric curiosity; it finds practical applications in various fields, from art and design to engineering and construction.

Its inherent symmetry and structural stability make it a desirable shape in tessellations, patterns, and decorative elements. Its predictable angles and side lengths make it easier to use in structures and mechanical designs. From diamond patterns in textiles to structural components in bridges, the rhombus's presence is both subtle and significant.

By appreciating the properties and applications of the rhombus, we gain a deeper understanding of the interconnectedness of geometry and the world around us.

Squares: The Ultimate Quadrilateral

As we ascend the hierarchy of quadrilaterals, we arrive at the pinnacle: the square. This seemingly simple shape embodies the most refined combination of properties, making it a uniquely elegant and powerful figure in geometry.

The square isn't just another quadrilateral; it's the culmination of all that comes before, inheriting the best characteristics of its predecessors.

Defining Perfection: The Square's Dual Identity

What precisely elevates a quadrilateral to square status? The answer lies in its dual heritage. A square can be defined in two equally valid ways, each highlighting its special relationship to other quadrilaterals.

Firstly, a square is a Rectangle with four equal sides. In other words, it takes the defining characteristic of a rectangle – four right angles – and adds the requirement of equal side lengths.

Alternatively, a square is a Rhombus with four right angles. Here, the square begins with the rhombus's hallmark of equal sides and incorporates the rectangle's right-angled precision.

Both definitions are equivalent and underscore the square's position as a hybrid, a perfect blend of rectangular and rhombic qualities.

A Legacy of Properties: Inheriting Geometric Excellence

Because the square is both a rectangle and a rhombus, it inherits all the properties of these shapes, along with those of the parallelogram, the foundation upon which they are built.

This means that a square possesses:

• Two pairs of parallel sides (parallelogram property).

• Opposite sides that are equal (parallelogram & rectangle property).

• Opposite angles that are equal (parallelogram & rhombus property).

• Four right angles (rectangle property).

• Four equal sides (rhombus property).

• Diagonals that bisect each other (parallelogram, rectangle, & rhombus property).

• Diagonals that are congruent (rectangle property).

• Diagonals that are perpendicular (rhombus property).

No other quadrilateral can boast such a complete set of characteristics.

The Epitome of Symmetry: A Perfectly Balanced Shape

The square's unique combination of properties leads to an unparalleled degree of symmetry. It exhibits:

• Rotational Symmetry: A square can be rotated 90, 180, or 270 degrees about its center and still look identical to its original orientation. This fourfold rotational symmetry is a testament to its balanced form.

• Reflectional Symmetry: A square possesses four lines of symmetry: two bisecting opposite sides and two running diagonally between opposite vertices. This allows it to be mirrored across these lines with no visible change.

This exceptional symmetry, stemming from its equal sides and right angles, further solidifies the square's position as a uniquely harmonious and balanced geometric figure.

The square, therefore, represents the culmination of quadrilateral evolution. It is a shape where equality and order converge, creating a figure of striking beauty and profound geometric significance.

Kites: Adjacent Sides and Symmetry

Stepping outside the parallelogram family, we encounter a captivating quadrilateral with a unique set of properties: the kite. Unlike its parallel-sided cousins, the kite's defining feature lies in its adjacent sides, creating a distinctive shape with its own special symmetries.

Defining the Kite: Adjacent Equality

A kite, at its core, is a quadrilateral defined by having two distinct pairs of adjacent sides that are equal in length. In simpler terms, imagine two isosceles triangles sharing a common base; the resulting figure is a kite.

It's crucial to note that while adjacent sides are equal, opposite sides are not. This is a key differentiator from parallelograms, rhombuses, and squares.

Properties Unveiled: More Than Just a Pretty Shape

The kite's unique construction gives rise to a fascinating array of properties that set it apart from other quadrilaterals.

Angle Relationships

One of the most notable properties is that exactly one pair of opposite angles are equal. The angles formed where the unequal sides meet are congruent.

The other pair of opposite angles are, in general, not equal. However, there is a special case when all angles are equal, the kite then becomes a square.

Diagonal Dynamics

The diagonals of a kite exhibit a special relationship. The longer diagonal, often referred to as the principal diagonal, bisects the shorter diagonal.

Furthermore, the diagonals intersect at right angles, meaning they are perpendicular to each other. This perpendicularity is a direct consequence of the kite's symmetry.

Symmetry in Action

Kites possess a single line of symmetry, which runs along the principal diagonal. This line divides the kite into two congruent triangles.

This symmetry dictates that the principal diagonal also bisects the two angles at the vertices it connects. It acts as an angle bisector for those two angles.

Kites in the Real World: Beyond Geometry Class

The kite shape isn't confined to the abstract world of geometry; it appears in various real-world applications. Of course, there are actual kites.

Look closely, and you'll find it in the design of certain tiles, logos, and even in architectural elements, leveraging its unique aesthetic appeal and structural properties.

Understanding kites expands our appreciation for the diversity and elegance found within the world of quadrilaterals. They are a reminder that geometry is not just about parallel lines and right angles; it's about exploring the endless possibilities that arise from different combinations of sides and angles.

Classification and Hierarchy: Organizing the Shapes

Understanding the world of quadrilaterals isn't merely about memorizing definitions; it's about grasping the underlying principles of classification and hierarchy. These principles provide a framework for organizing shapes, revealing the intricate relationships that connect seemingly disparate figures.

The Power of Classification

At its core, classification is the process of grouping objects based on shared characteristics. In geometry, this means categorizing quadrilaterals according to their sides, angles, and, crucially, the presence (or absence) of parallel lines. This systematic organization isn't arbitrary; it's the foundation upon which the hierarchy of quadrilaterals is built.

Without this act of sorting and cataloging we’d never be able to make the broader geometric connections that form our knowledge base.

Sides, Angles, and Parallel Lines: The Classifiers

The properties of sides, angles, and the presence (or absence) of parallel lines are the key determinants in classifying quadrilaterals.

Does the quadrilateral have any parallel sides? Are all sides equal in length? Are all angles right angles?

The answers to these questions dictate a quadrilateral's position within the hierarchy. These criteria are not of equal weight, as the presence of parallel lines is of primary importance.

A trapezoid, for instance, requires only one pair of parallel sides, while a parallelogram demands two. This seemingly small difference places these shapes in distinct, though related, categories.

The Quadrilateral Family Tree: A Visual Representation

A visual representation, often depicted as a diagram or "family tree," is invaluable for understanding the quadrilateral hierarchy. The diagram highlights the relationships, with the broadest categories (like quadrilaterals and trapezoids) at the top, branching down to more specialized shapes (like squares) at the bottom.

Quadrilaterals sit at the top as the most general category. Below are Trapezoids which need at least one set of parallel lines. Then comes Parallelograms, Kites, Rhombuses, and Rectangles. Finally, the Square is the most specialized as it inherits all the properties above.

These diagrams make it easy to see how a square is also a rectangle, a rhombus, and a parallelogram. The order highlights how categories descend from one another.

This visual tool provides an intuitive understanding of how the different types of quadrilaterals are related, how they descend from one another and makes the material less of a memorization exercise and more of a process of understanding the underlying relationships.

The Significance of Quadrilaterals: Applications and Importance

Quadrilaterals are more than just textbook figures; they are fundamental building blocks of our physical and conceptual world. Their ubiquitous presence often goes unnoticed, yet they are essential to our understanding of geometry and its applications.

The Cornerstone of Geometric Proofs

Before any practical application, understanding quadrilaterals is paramount for grasping geometric proofs. The precise definitions of shapes like squares, rectangles, and trapezoids aren't arbitrary; they're the bedrock upon which complex geometric arguments are constructed.

To rigorously demonstrate why certain geometric relationships hold true, we rely on the established definitions and properties of quadrilaterals. Without understanding a quadrilateral's definition, a geometric proof is impossible.

This understanding begins with the fundamental definition of a quadrilateral itself – a polygon with four sides and four angles. From there, we build upon this definition.

Quadrilaterals in Architecture, Engineering, and Design

The properties of angles and sides of quadrilaterals are directly leveraged in architecture, engineering, and design. The inherent stability of triangles is often augmented using quadrilaterals, particularly rectangles and squares, to form robust structures.

The precise right angles in rectangles are crucial for creating stable walls and floors. The equal sides of squares ensure uniformity and predictability in construction.

Engineers rely on the predictable geometric properties of quadrilaterals. These properties are used for calculating load distribution and structural integrity in bridges and buildings.

Designers, on the other hand, use quadrilaterals for aesthetic purposes. These shapes are for crafting visually appealing and balanced compositions, both in physical spaces and digital interfaces.

The Geometry Textbook: A Foundation of Knowledge

Geometry textbooks play a crucial role in establishing a common understanding of quadrilaterals. These books provide standardized definitions and properties of quadrilaterals.

This standardization allows for clear communication and collaboration within the fields of mathematics, engineering, and architecture. Textbooks provide the core language.

Without this shared understanding, more abstract geometrical discussion would become rife with ambiguity. Thus, they serve as more than just repositories of information.

Everyday Quadrilaterals: A World of Shapes

Quadrilaterals are not confined to the realm of textbooks and mathematical equations. They are everywhere around us. Look at windows, tiles, tables, and even the screens you are reading this on.

The rectangular shape of a window allows for efficient use of space and provides a clear view of the outside world. Tiles, often in the form of squares or rectangles, create patterns and surfaces that are both functional and aesthetically pleasing.

The stable base of a table is often achieved through a quadrilateral design, providing a surface for work, dining, or display. These are all testaments to the practicality and versatility of quadrilaterals.

Video: Are All Quadrilaterals Trapezoids? Geometry Truth

Play Video

So, are all quadrilaterals trapezoids? Hopefully, now you see that while it's tempting to lump them all together, the geometry truth reveals that only quadrilaterals with at least one pair of parallel sides can truly claim the trapezoid title. Keep exploring those shapes and remember, geometry's full of fascinating little details like this!