Unlock the Quadrilateral Family Tree: A Visual Guide

Geometry, a branch of mathematics, provides the foundational principles for understanding shapes. The Khan Academy resource offers numerous tutorials for grasping geometric concepts. The quadrilateral family tree, a visual representation, effectively categorizes various quadrilaterals based on their properties. Euclid's Elements, an ancient mathematical text, originally laid the groundwork for many of the geometric theorems that define the quadrilateral family tree. Exploring the quadrilateral family tree allows learners to efficiently classify shapes.

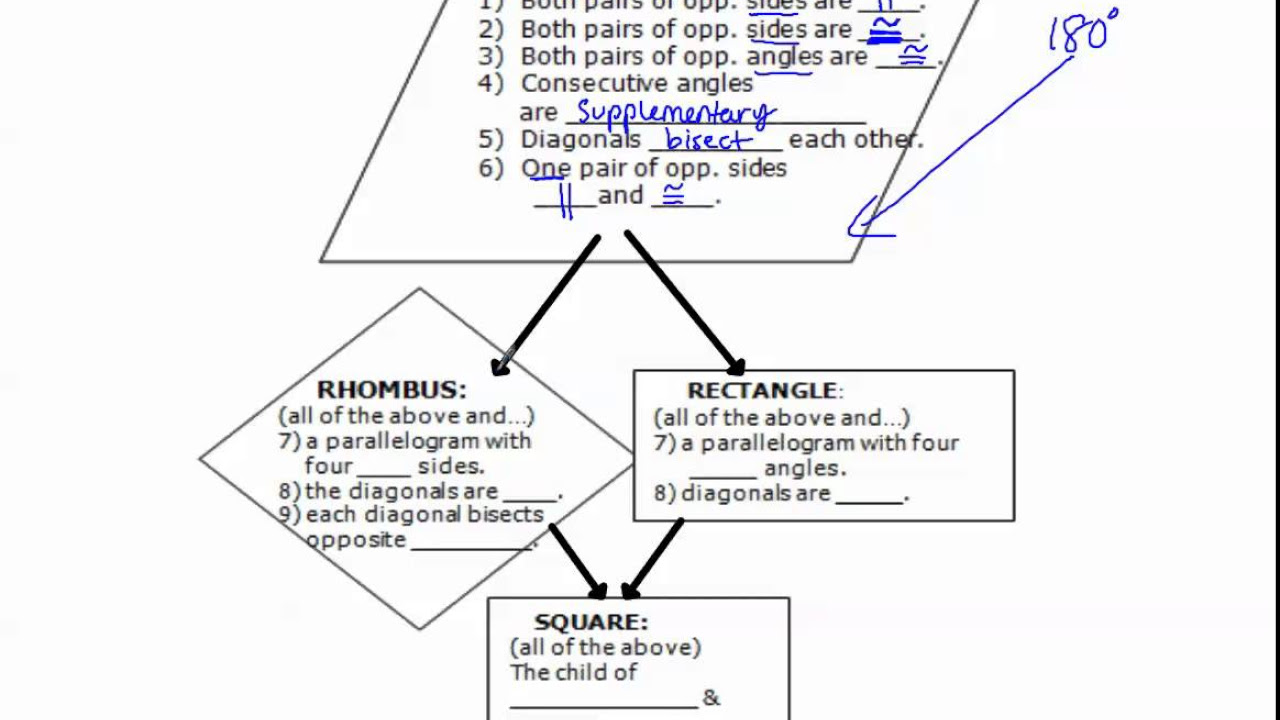
Image taken from the YouTube channel Marshematics , from the video titled Quadrilateral Family Tree .

Unveiling the Quadrilateral Family Tree

Quadrilaterals, those four-sided figures that populate our geometric landscape, are more than just simple shapes. They are, in essence, the fundamental building blocks upon which more complex geometric structures are built. From the squares and rectangles that form the basis of architecture to the rhombuses and trapezoids that appear in tessellations and design, quadrilaterals are ubiquitous.

The Importance of Classification

Understanding the classification of quadrilaterals, and more importantly, the relationships between them, is paramount for several reasons:

• Enhanced Geometric Reasoning: By grasping the properties that define each type of quadrilateral, we sharpen our ability to reason geometrically.
• Problem-Solving Prowess: Recognizing the specific characteristics of a shape allows us to apply the correct formulas and theorems to solve problems.
• Appreciation of Mathematical Structure: Understanding the hierarchy of quadrilaterals reveals the elegant structure and interconnectedness within geometry.

Visualizing Relationships: The Family Tree Analogy

To aid in this understanding, we introduce the analogy of a "family tree." Just as a family tree illustrates the relationships between individuals, the quadrilateral family tree visually represents the connections between different types of quadrilaterals.

This tree highlights how certain quadrilaterals inherit properties from their "ancestors" while also developing unique characteristics of their own. For example, a square is a special type of rectangle, which in turn is a special type of parallelogram.

A Clear Guide to the Quadrilateral Landscape

This article serves as a clear and accessible guide to navigating the quadrilateral family tree. We aim to provide a comprehensive overview of the different types of quadrilaterals, their defining properties, and the relationships that bind them together.

By the end of this exploration, you will have a solid understanding of the quadrilateral landscape and be able to confidently identify and classify these essential geometric shapes.

Laying the Foundation: What Defines a Quadrilateral?

Before we can effectively navigate the branches and leaves of the quadrilateral family tree, we must first establish a firm foundation. Understanding the fundamental definition of a quadrilateral and the properties shared by all its members is crucial. This groundwork allows us to appreciate the nuances that differentiate specific types of quadrilaterals later on.

The Mathematical Definition of a Quadrilateral

At its core, a quadrilateral is defined as a closed, two-dimensional shape formed by four straight line segments. These line segments are called sides, and the points where they meet are called vertices (singular: vertex).

A quadrilateral also possesses four angles, formed by the intersection of its sides at the vertices. This seemingly simple definition encapsulates the essence of all shapes that fall under the quadrilateral umbrella.

Shared Geometric Properties

While quadrilaterals exhibit a wide variety of shapes and sizes, they all share certain fundamental geometric properties. One of the most important is the sum of their interior angles.

In Euclidean geometry, the sum of the interior angles of any quadrilateral is always 360 degrees. This is a constant, regardless of whether the quadrilateral is a square, a trapezoid, or an irregular shape.

Another shared property relates to the sides and vertices: Every quadrilateral has four sides and four vertices. This might seem obvious, but it's a defining characteristic that distinguishes quadrilaterals from other polygons, such as triangles (three sides) or pentagons (five sides).

Euclidean Geometry as the Framework

Our understanding of quadrilaterals, and indeed most of elementary geometry, is rooted in Euclidean geometry. This system, developed by the ancient Greek mathematician Euclid, provides the axioms and postulates upon which we build our geometric knowledge.

Euclidean geometry assumes a flat, two-dimensional space, where lines are perfectly straight and parallel lines never intersect. These assumptions are fundamental to the properties and theorems we use to analyze quadrilaterals.

Key Concepts: Sides, Angles, and Diagonals

To delve deeper into the world of quadrilaterals, it's essential to understand a few key concepts: sides, angles, and diagonals.

Sides are the line segments that form the boundary of the quadrilateral. Their lengths and relationships to each other are crucial in classifying different types of quadrilaterals.

Angles are formed at the vertices where the sides meet. As mentioned earlier, the sum of the interior angles is always 360 degrees, but the individual angle measures can vary greatly.

A diagonal is a line segment that connects two non-adjacent vertices of the quadrilateral. Every quadrilateral has two diagonals. Diagonals play a significant role in determining the properties of certain quadrilaterals, such as parallelograms and rhombuses.

The Main Branches: Introducing Key Quadrilateral Types

Having laid the groundwork with a fundamental understanding of what defines a quadrilateral, we can now begin to explore the diverse landscape of specific quadrilateral types. The world of quadrilaterals is far from a monotonous collection of four-sided shapes; it is a rich tapestry woven with distinct categories, each possessing unique properties and characteristics.

Categorizing the Quadrilateral Family

The organization of the quadrilateral family is not arbitrary. It is based on a system of classification that considers both shared geometric properties and unique attributes. Certain quadrilaterals share fundamental traits, such as having parallel sides, equal angles, or specific diagonal relationships.

These shared characteristics form the basis for grouping them into broader categories. Within these categories, further distinctions arise from additional properties, leading to a hierarchical structure that resembles a family tree.

A Hierarchy of Properties

This "family tree" isn't just a visual aid; it reflects a deeper mathematical reality. Quadrilaterals higher up in the tree possess more general properties, while those lower down inherit those properties and gain additional, more specific ones. This inheritance creates clear lineages and relationships between different shapes.

Understanding this hierarchy is key to mastering the classification of quadrilaterals. By recognizing the defining properties of each category, we can accurately identify and classify any quadrilateral we encounter.

Key Quadrilateral Categories: A Preview

As we ascend the quadrilateral family tree, several prominent branches emerge. These represent the major categories of quadrilaterals, each distinguished by its own set of defining characteristics.

Some of the most important branches we will be exploring include:

• Parallelograms: Defined by having two pairs of parallel sides.

• Trapezoids (US) / Trapeziums (UK): Characterized by having at least one pair of parallel sides.

• Kites: Distinguished by having two pairs of adjacent sides that are equal in length.

These categories serve as the foundation for understanding the relationships between various quadrilaterals. Each branch gives rise to further classifications, yielding shapes with increasingly specialized properties. In subsequent sections, we will delve into each of these branches in greater detail, unveiling the unique characteristics and relationships that define the quadrilateral family tree.

Having established a foundational understanding of the quadrilateral family and its major categories, we now turn our attention to one of its most prominent and well-defined branches: the parallelogram. This family of shapes is characterized by its unique property of having two pairs of parallel sides, a feature that gives rise to a host of other interesting geometric relationships. Let's delve into the specifics of what defines a parallelogram and explore the characteristics that make it such an important shape in geometry.

The Parallelogram Branch: Exploring Parallel Sides

At the heart of the quadrilateral family lies the parallelogram, a versatile shape defined by its parallel sides. But what exactly makes a parallelogram unique, and what properties arise from this defining characteristic?

Defining the Parallelogram: A Matter of Parallelism

A parallelogram is formally defined as a quadrilateral with two pairs of parallel sides. This seemingly simple definition has profound implications for the shape's other attributes.

It is essential to not confuse a parallelogram with other quadrilaterals. The critical distinction lies in that both pairs of opposite sides must be parallel. If only one pair is parallel, we're dealing with a trapezoid (or trapezium, depending on your region).

Key Geometric Properties of Parallelograms

The parallel nature of a parallelogram's sides gives rise to several notable geometric properties:

• Equal Opposite Sides and Angles: In any parallelogram, the opposite sides are equal in length, and the opposite angles are equal in measure. This symmetry is a direct consequence of the parallel lines and their transversal relationships.

• Bisecting Diagonals: The diagonals of a parallelogram bisect each other. This means that the point where the two diagonals intersect is the midpoint of each diagonal. This property is incredibly useful in various geometric proofs and constructions.

These properties are not merely interesting observations; they are fundamental characteristics that can be used to identify parallelograms and solve geometric problems.

Relationships Within the Parallelogram Branch

The parallelogram branch of the quadrilateral family isn't just a single shape; it's a parent category encompassing several important "descendants." Shapes such as rectangles, squares, and rhombuses are all special types of parallelograms, each with additional constraints and properties that build upon the basic parallelogram structure.

These relationships create a hierarchical structure where the properties of the parent (parallelogram) are inherited by its children (rectangles, squares, rhombuses), while the children gain unique properties of their own. Understanding this hierarchy is crucial for fully grasping the interconnectedness of the quadrilateral family.

Having explored the foundational characteristics of parallelograms, the natural progression is to examine their direct descendants: rectangles, squares, and rhombuses. These shapes inherit the core properties of parallelograms but possess additional defining attributes that set them apart. Understanding these distinctions is crucial for a comprehensive grasp of quadrilateral geometry.

Descendants of the Parallelogram: Rectangles, Squares, and Rhombuses Explained

The parallelogram family branches into several specialized shapes, each building upon the fundamental properties of its ancestor. Rectangles, squares, and rhombuses are all parallelograms, but with added constraints that lead to unique geometric characteristics. This section explores each of these shapes in detail, highlighting both their shared heritage and their individual identities.

Rectangles: Right Angles and Inherited Traits

A rectangle is defined as a parallelogram with four right angles. This seemingly simple addition has significant consequences for its properties.

Inheritance and Augmentation

Rectangles inherit all the properties of parallelograms: opposite sides are parallel and equal in length, opposite angles are equal, and diagonals bisect each other.

However, the presence of four right angles introduces a new level of symmetry and predictability. Each angle measures 90 degrees, and consequently, the diagonals of a rectangle are equal in length. This is a property not shared by all parallelograms.

Squares: The Epitome of Regularity

The square occupies a special position in the quadrilateral family tree.

It is often described as a regular quadrilateral, meaning it is both equilateral (all sides equal) and equiangular (all angles equal).

A Synthesis of Properties

A square can be viewed as both a rectangle with four equal sides or a rhombus with four right angles. This dual inheritance means that squares possess all the properties of both rectangles and rhombuses.

Its diagonals are equal in length (like a rectangle), bisect each other at right angles (like a rhombus), and bisect the angles of the square (45-degree angles). The square's high degree of symmetry makes it a fundamental shape in geometry and construction.

Rhombuses: Equal Sides and Angular Bisection

A rhombus (plural: rhombuses or rhombi) is a parallelogram with four equal sides.

While its angles are not necessarily right angles, the equality of its sides leads to distinct properties related to its diagonals.

Diagonals and Symmetry

The diagonals of a rhombus bisect each other at right angles. This is a key characteristic that distinguishes it from a general parallelogram. Furthermore, the diagonals of a rhombus also bisect its angles, dividing each angle into two equal parts. This property stems from the rhombus's inherent symmetry and the equality of its sides.

Having charted the course through parallelograms and their uniquely shaped descendants, it's time to set sail for another significant branch of the quadrilateral family: the trapezoid (in US terminology) or trapezium (in UK terminology). These shapes, while distinct from parallelograms, possess their own set of fascinating properties and variations, solidifying their place in the broader landscape of four-sided figures.

The Trapezoid (US) / Trapezium (UK) Branch: One Pair of Parallel Sides

At its core, the defining characteristic of a trapezoid (or trapezium) is that it is a quadrilateral possessing at least one pair of parallel sides.

This single criterion sets it apart from parallelograms, which, as we've explored, require two pairs of parallel sides.

This seemingly small difference has major consequences for the properties and behaviors of these shapes.

Defining the Trapezoid/Trapezium: A Singular Requirement

Let's solidify the definition. A trapezoid (US) or trapezium (UK) is a closed, two-dimensional shape, adhering to the fundamental definition of a quadrilateral: four sides and four angles.

However, what elevates it to the status of a trapezoid/trapezium is the presence of one, and only one, pair of parallel sides.

These parallel sides are often referred to as the bases of the trapezoid/trapezium.

The non-parallel sides are known as the legs, or lateral sides.

Trapezoids/Trapeziums vs. Parallelograms: A Tale of Parallelism

The key difference between trapezoids/trapeziums and parallelograms lies in the number of parallel side pairs. Parallelograms must have two pairs of parallel sides.

In contrast, trapezoids/trapeziums are defined by having only one.

If a quadrilateral possesses two pairs of parallel sides, it automatically qualifies as a parallelogram, thereby excluding it from the trapezoid/trapezium category.

It is this lack of a second pair of parallel sides that dictates the unique properties and characteristics of trapezoids/trapeziums, distinguishing them from their parallelogram cousins.

Varieties Within the Branch: Exploring Trapezoid/Trapezium Types

The trapezoid/trapezium family isn't monolithic. Several distinct types exist, each distinguished by additional properties beyond the fundamental parallel side requirement.

Isosceles Trapezoids/Trapeziums

Perhaps the most well-known variation is the isosceles trapezoid/trapezium.

In addition to having one pair of parallel sides, an isosceles trapezoid/trapezium features legs of equal length.

This equality of leg lengths leads to further interesting properties. The base angles (angles formed by a base and a leg) are equal in measure. The diagonals are also equal in length.

These added symmetries elevate the isosceles trapezoid/trapezium to a special status within the broader family.

Right Trapezoids/Trapeziums

Another notable type is the right trapezoid/trapezium.

As the name suggests, a right trapezoid/trapezium has at least one right angle.

In practice, it must have two right angles, since a trapezoid has one pair of parallel sides.

These right angles are adjacent to one of the bases, creating a shape that combines the defining characteristic of a trapezoid/trapezium with the perpendicularity of a right angle.

Scalene Trapezoids/Trapeziums

Finally, we have scalene trapezoids/trapeziums. These are trapezoids/trapeziums where the legs are of unequal length and none of the angles are right angles.

They represent the "default" or most general form of a trapezoid/trapezium, lacking the special properties of the isosceles or right varieties.

They still meet the basic definition of having one pair of parallel sides.

Having explored the individual branches of the quadrilateral family, from the strict parallelism of parallelograms to the singular parallel sides of trapezoids, it's time to step back and view the entire landscape. To truly grasp the intricate relationships between these shapes, a visual representation becomes invaluable.

Visualizing the Family Tree: Diagrams and Charts for Clarity

Geometric relationships can often feel abstract. Visual aids, such as diagrams and charts, provide a concrete framework for understanding how different quadrilaterals relate to one another. They transform abstract concepts into tangible visual representations, making the hierarchical structure of the quadrilateral family more accessible and memorable.

The Power of Visual Representation

The human brain is wired to process visual information effectively. Diagrams and charts leverage this innate ability to simplify complex information. By representing quadrilaterals and their properties visually, we can quickly identify commonalities and differences, and more effectively internalize their relationships.

Unveiling Hierarchy with Diagrams

Visual aids, especially hierarchical charts, excel at revealing the inherent hierarchy within the quadrilateral family. For instance, a chart can clearly illustrate that squares are a subset of both rectangles and rhombuses, which are in turn subsets of parallelograms, and so on. This top-down representation makes it easier to understand the inheritance of properties as we move down the "family tree."

Venn Diagrams: Spotlighting Overlapping Properties

Venn diagrams provide another powerful tool for visualizing the relationships between quadrilaterals. By using overlapping circles to represent different types of quadrilaterals, Venn diagrams visually highlight the shared properties between them. The overlapping region between the "Rectangle" and "Rhombus" circles, for example, immediately reveals the defining characteristics of a square. This visual overlap drives home the concept that a square embodies the properties of both its parent shapes.

Examples of Effective Visual Aids

• Hierarchical Charts (Family Trees): These charts display the classification of quadrilaterals in a tree-like structure, showing how different types are related to each other. The most general category (quadrilaterals) sits at the top, with more specific types branching out below.

• Venn Diagrams: Venn diagrams use overlapping circles to illustrate shared properties between different quadrilateral types. The overlapping areas represent quadrilaterals that possess properties of multiple categories.

• Property Charts: These charts list the key properties of each quadrilateral type in a table format. This allows for easy comparison and identification of similarities and differences.

  You also like

  Building Blocks of Tissues: Cells & Matrix Guide

By embracing the power of visual aids, we can transform the complex landscape of quadrilaterals into a clear and intuitive structure. These tools are essential for truly mastering the relationships within the quadrilateral family, fostering a deeper understanding of geometric principles.

Video: Unlock the Quadrilateral Family Tree: A Visual Guide

Play Video