Unlock the d Sublevel! How Many Orbitals Exist?! ⚛️

Delving into the intricacies of quantum mechanics, we often encounter the d sublevel, a crucial component in understanding electron configuration and chemical bonding. The d sublevel's properties are especially important when considering the behavior of transition metals, which exhibit diverse oxidation states due to the filling of their d orbitals. Central to this understanding is the number of orbitals for the d sublevel is five, a fact underpinning many chemical phenomena. These five d orbitals have characteristic shapes and spatial orientations, influencing the geometries of coordination complexes. Linus Pauling, a pioneer in chemical bonding theory, highlighted the significance of understanding these orbitals in predicting molecular structures. Modern computational chemistry, facilitated by software such as Gaussian, enables scientists to visualize and model these d orbitals, further solidifying our grasp of their roles.

Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Orbitals, Atomic Energy Levels, & Sublevels Explained - Basic Introduction to Quantum Numbers .

Unveiling the Mysteries of the d Sublevel

Why are transition metals so vibrantly colored?

What gives them their remarkable ability to catalyze reactions, acting as essential workhorses in countless industrial processes?

The answers lie hidden within the intricate dance of electrons, specifically, within the enigmatic d sublevel.

The Atom: A Foundation of Understanding

At the heart of matter lies the atom, a microcosm of energy and interactions. Understanding its structure is paramount to unraveling the secrets of chemical behavior.

Imagine the atom as a miniature solar system, with a central nucleus containing protons and neutrons, orbited by electrons.

These electrons aren't just randomly scattered; they occupy specific energy levels and regions of space known as electron orbitals.

The arrangement of electrons within these orbitals dictates an atom's properties, influencing how it bonds with other atoms and its overall reactivity.

Orbitals: The Electron's Address

Electron orbitals are not fixed paths like planetary orbits. Instead, they represent regions of probability where an electron is most likely to be found.

These orbitals come in various shapes and sizes, each corresponding to a specific energy level.

The properties of an atom and its interactions are, in essence, a result of the number of electrons it contains and the specific orientations of these electrons.

This is often referred to as the electron configuration.

The Curious Case of the d Sublevel: Our Quantum Quest

Within the atom, energy levels are further divided into sublevels, designated as s, p, d, and f.

This exploration focuses on the d sublevel, a region of space that holds a unique set of orbitals.

How many orbitals reside within the d sublevel, and what implications does this number have on the properties of elements?

We will delve into the quantum world to decode the secrets of the d sublevel, revealing its connection to quantum numbers and its significance in the realm of quantum mechanics.

This article will illuminate the number of orbitals in the d sublevel, link it to quantum numbers, and underscore its significance in quantum mechanics.

Unraveling the atom's secrets requires more than just a conceptual model; it demands a precise language, a system for defining the characteristics of electrons. This is where quantum numbers enter the stage, providing a detailed description of each electron's state within the atom. Let's delve into the world of these numbers.

Diving into the Quantum World: Quantum Numbers Decoded

The behavior of electrons within an atom is governed by the principles of quantum mechanics. To fully describe an electron's state, we use a set of four fundamental quantum numbers.

These numbers provide a unique "address" for each electron, defining its energy level, shape of its orbital, spatial orientation, and intrinsic angular momentum (spin).

Understanding these numbers is crucial for predicting and explaining the chemical properties of elements.

The Four Quantum Numbers: A Complete Electron Profile

Let's break down each of the four quantum numbers:

• Principal Quantum Number (n): This number defines the energy level of an electron. It can be any positive integer (n = 1, 2, 3, ...), with higher numbers indicating higher energy levels and greater distances from the nucleus. Think of it as the "shell" where the electron resides.

• Azimuthal Quantum Number (l): Also known as the angular momentum or orbital shape quantum number, 'l' determines the shape of an electron's orbital and has values ranging from 0 to n-1. For n = 1, l can only be 0; for n = 2, l can be 0 or 1, and so on. The specific shape defines a sublevel.

• Magnetic Quantum Number (ml): This number specifies the orientation of an electron's orbital in space. For a given value of 'l', ml can take on values from -l to +l, including 0. The number of possible ml values indicates the number of orbitals within a sublevel.

  You also like

  Ram Secrets: Everything You Need to Know About Male Sheep!

• Spin Quantum Number (ms): This number describes the intrinsic angular momentum of an electron, which is quantized and referred to as spin. An electron behaves as if it is spinning, creating a magnetic dipole moment. It can only have two possible values: +1/2 or -1/2, often referred to as "spin up" and "spin down."

The Azimuthal Quantum Number (l): Shaping the Electron's World

The azimuthal quantum number, denoted as 'l', is paramount in determining the shape of an electron's orbital. This shape profoundly influences how an atom interacts with other atoms, forming chemical bonds and dictating molecular geometry.

For a given principal quantum number (n), 'l' can take on values ranging from 0 to n-1. Each value of 'l' corresponds to a specific sublevel within the electron shell:

• l = 0 corresponds to an s sublevel, which has a spherical shape.

• l = 1 corresponds to a p sublevel, which has a dumbbell shape.

• l = 2 corresponds to a d sublevel, which has more complex shapes (as we will see later).

• l = 3 corresponds to an f sublevel, which has even more intricate shapes.

Connecting 'l' to Sublevels: s, p, d, and f

The azimuthal quantum number directly determines the type of sublevel an electron occupies:

When l = 0, we have the s sublevel. When l = 1, we have the p sublevel. When l = 2, we have the d sublevel. When l = 3, we have the f sublevel.

These sublevels represent different regions of space where an electron is most likely to be found, each with its characteristic shape and energy.

The d Sublevel: l = 2

For the d sublevel, the azimuthal quantum number, l, is equal to 2. This single piece of information unlocks a wealth of knowledge about the d sublevel's properties, including the number and shapes of its orbitals, which in turn dictates behavior in the quantum world.

Unlocking the d Sublevel: Shape, Orientation, and the Magic Number 5

Having established the framework of quantum numbers and their roles in defining electron behavior, we can now focus our attention on a specific and incredibly important sublevel: the d sublevel. It's within this sublevel that we begin to see the emergence of fascinating chemical properties, particularly those associated with transition metals. So, what exactly makes the d sublevel so special, and how many orbitals does it contain?

The Magnetic Quantum Number and Spatial Orientation

While the azimuthal quantum number (l) dictates the shape of an orbital, the magnetic quantum number (ml) governs its orientation in space. Think of it as the compass that directs each orbital along a specific axis. For a given value of l, ml can take on values ranging from -l to +l, including 0. This range determines the number of orbitals within that particular sublevel.

The magnetic quantum number reveals how many orientations a given orbital shape can adopt in three-dimensional space. Each unique value of ml corresponds to a distinct orbital residing within the sublevel.

Decoding the Number of d Orbitals: The Formula

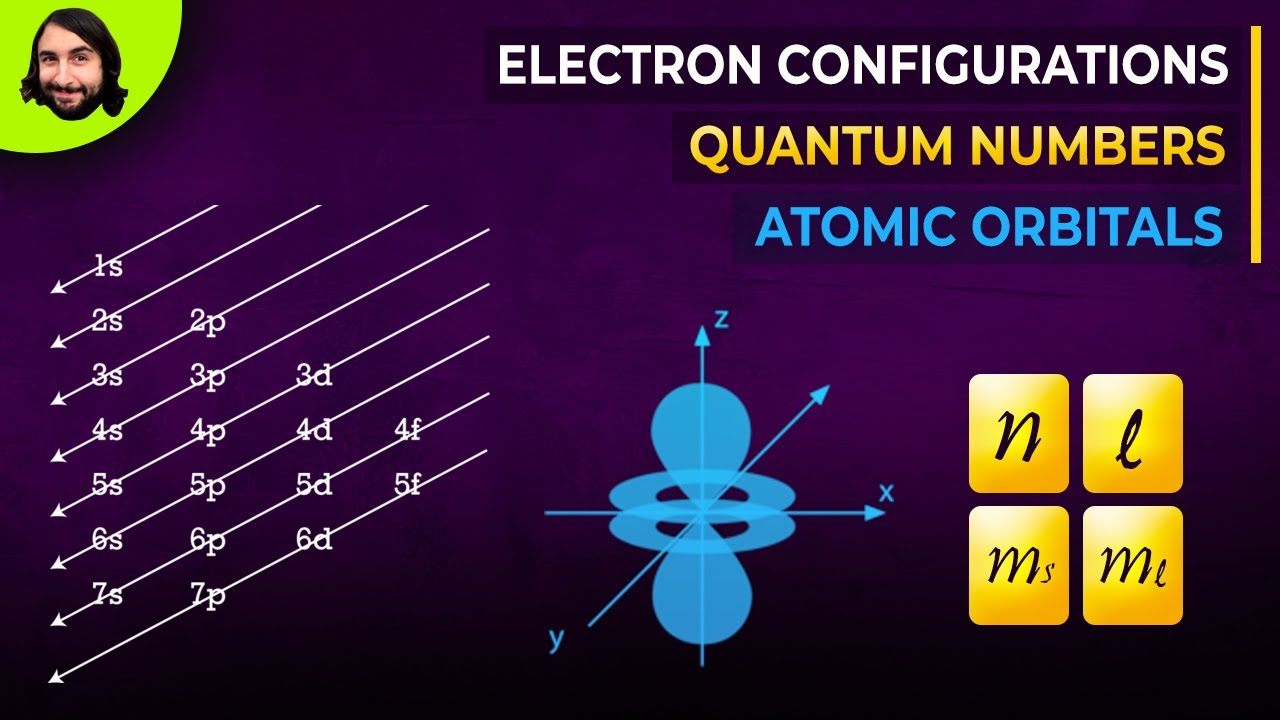
The relationship between the azimuthal quantum number (l) and the number of orbitals in a sublevel is defined by the simple equation: 2l + 1. This is a crucial formula for understanding the architecture of electron orbitals.

For the d sublevel, l = 2. Plugging this value into the equation, we get: 2(2) + 1 = 5.

Therefore, the d sublevel contains five orbitals. This "magic number 5" is at the heart of many unique properties exhibited by elements with electrons occupying these orbitals.

Visualizing the Five d Orbitals: Shapes and Spatial Arrangements

Each of the five d orbitals possesses a distinct spatial orientation and a characteristic shape, more complex than the s and p orbitals. While a precise mathematical description requires advanced quantum mechanics, we can visualize their approximate forms:

• dxy, dxz, dyz: These three orbitals have a similar "four-leaf clover" shape. Each "leaf" points between the respective x and y, x and z, and y and z axes, respectively.

• dx2-y2: This orbital also features a four-leaf clover shape. However, unlike the previous three, its "leaves" align directly along the x and y axes.

• dz2: This orbital is unique, resembling a dumbbell shape along the z-axis, with a "doughnut" or ring encircling the dumbbell in the xy-plane.

Visual representations of these orbitals are crucial for developing a deeper understanding of their spatial distributions.

Understanding these shapes and spatial orientations helps us predict how d orbitals will interact with other atoms and molecules, thereby influencing chemical bonding and reactivity. The spatial arrangement also underlies many of the properties exhibited by coordination compounds and transition metal complexes.

Electron Configuration: Filling the d Sublevel's Seats

Having established that the d sublevel houses five distinct orbitals, the next logical question is: how are these orbitals populated with electrons? The answer lies in the concept of electron configuration, the roadmap that dictates how electrons arrange themselves within an atom's energy levels and orbitals. Understanding these arrangements is critical for predicting and explaining the chemical behavior of elements, particularly the fascinating properties of transition metals.

The Electron Configuration Blueprint

Electron configuration is essentially a shorthand notation that describes the distribution of electrons among the various atomic orbitals. It follows a specific format: the principal quantum number (n), representing the energy level, is followed by the letter denoting the sublevel (s, p, d, or f), and a superscript indicating the number of electrons in that sublevel.

For example, the electron configuration of hydrogen is 1s¹, indicating that it has one electron in the s sublevel of the first energy level. As atoms become more complex, filling orbitals becomes governed by a set of fundamental principles.

Rules of Engagement: Filling Orbitals the Right Way

Several rules govern how electrons fill atomic orbitals, ensuring the most stable and energetically favorable arrangement. These rules are the Aufbau principle, Hund's Rule, and the Pauli Exclusion Principle.

The Aufbau Principle: Building Up from the Ground

The Aufbau principle, derived from the German word for "building up," dictates that electrons first occupy the lowest energy orbitals available before filling higher energy ones. This might seem straightforward, but the energy levels of orbitals can sometimes overlap, especially for higher energy levels and sublevels.

A helpful tool for predicting the filling order is the diagonal rule, which provides a visual guide for determining the sequence in which orbitals are filled. Note that exceptions to the Aufbau principle exist, particularly with transition metals, due to the subtle energy differences between orbitals.

Hund's Rule: Maximizing Multiplicity

Hund's Rule comes into play when filling orbitals within a sublevel that contains multiple orbitals of equal energy, such as the three p orbitals or the five d orbitals. This rule states that electrons will individually occupy each orbital within a sublevel before doubling up in any one orbital. Furthermore, these single electrons will all have the same spin (either spin-up or spin-down) to minimize electron-electron repulsion. This maximizes the total spin, hence why Hund's rule is sometimes referred to as the rule of maximum multiplicity.

The reason for this behavior is that electrons, being negatively charged, repel each other. By occupying separate orbitals with the same spin, electrons maximize the distance between them, minimizing their repulsive interactions and leading to a more stable configuration.

The Pauli Exclusion Principle: No Two Electrons Alike

The Pauli Exclusion Principle is a cornerstone of quantum mechanics, stating that no two electrons in an atom can have the same set of four quantum numbers. Since each orbital is defined by a unique set of n, l, and ml quantum numbers, and an electron has a spin quantum number of +1/2 or -1/2, this means that each orbital can hold a maximum of two electrons, with opposite spins.

This principle explains why each orbital can only accommodate two electrons, one with spin-up and one with spin-down. If a third electron were to occupy the same orbital, it would necessarily have the same set of all four quantum numbers as one of the other two electrons, violating the Pauli Exclusion Principle.

The d Sublevel in Action: Transition Metal Configurations

The d sublevel's five orbitals become especially important when considering the electron configurations of transition metals. These elements, found in the d-block of the periodic table, are characterized by having their outermost electrons filling the d orbitals.

This partially filled d sublevel is responsible for many of the unique properties associated with transition metals, such as their variable oxidation states, catalytic activity, and ability to form colored compounds. For example, consider iron (Fe), which has an electron configuration of [Ar] 3d⁶ 4s². The presence of six electrons in the 3d sublevel allows iron to form various ions with different oxidation states, such as Fe²⁺ and Fe³⁺, each exhibiting distinct chemical behavior.

Examples of Transition Metal Electron Configurations

Let's examine a few examples to illustrate how the d sublevel is filled in transition metals:

• Scandium (Sc): [Ar] 3d¹ 4s² (One electron in the 3d sublevel)
• Titanium (Ti): [Ar] 3d² 4s² (Two electrons in the 3d sublevel)
• Vanadium (V): [Ar] 3d³ 4s² (Three electrons in the 3d sublevel)
• Chromium (Cr): [Ar] 3d⁵ 4s¹ (An exception! Half-filled d sublevel is more stable)
• Manganese (Mn): [Ar] 3d⁵ 4s² (Five electrons in the 3d sublevel)
• Iron (Fe): [Ar] 3d⁶ 4s² (Six electrons in the 3d sublevel)
• Copper (Cu): [Ar] 3d¹⁰ 4s¹ (Another exception! Filled d sublevel is more stable)
• Zinc (Zn): [Ar] 3d¹⁰ 4s² (Completely filled d sublevel)

Note the exceptions for Chromium and Copper. These exceptions highlight the stability associated with half-filled and fully filled d sublevels. Chromium achieves a more stable configuration by promoting one electron from the 4s orbital to the 3d orbital, resulting in a half-filled 3d sublevel. Similarly, Copper achieves a filled 3d sublevel, further exemplifying the drive towards greater stability.

Understanding electron configuration provides a powerful framework for explaining the chemical properties and behaviors of elements. The filling of the d sublevel in transition metals is a prime example of how electron configuration dictates the unique characteristics of these important elements.

The Significance of the d Sublevel: Properties and Applications

The implications of those five d orbitals extend far beyond mere theoretical calculations. They underpin many of the most distinctive and useful properties of transition metals, elements that play a pivotal role in countless chemical processes and technological applications. Understanding the d sublevel is, therefore, key to unlocking the secrets of these fascinating elements.

Variable Oxidation States: A Consequence of d Orbital Flexibility

One of the most striking characteristics of transition metals is their ability to exhibit multiple oxidation states. Unlike main group elements, which typically have a fixed or limited number of oxidation states, transition metals can lose varying numbers of electrons from their d orbitals, leading to a wide range of stable ionic forms.

This versatility stems directly from the relatively small energy difference between the d orbitals and the s orbitals in the valence shell. Electrons can be readily removed or added to the d orbitals, allowing the metal to adopt the oxidation state that best suits the chemical environment.

This ability is crucial in many biological systems, where transition metals like iron and copper act as redox centers in enzymes, facilitating electron transfer reactions.

Catalytic Activity: Orchestrating Chemical Reactions

Transition metals and their compounds are renowned for their exceptional catalytic activity. This stems from the ability of d orbitals to form temporary bonds with reactant molecules, weakening existing bonds and facilitating the formation of new ones.

The availability of empty or partially filled d orbitals allows the metal center to act as a "staging ground" for chemical reactions, bringing reactants together in the optimal orientation for bond formation.

Heterogeneous catalysts, such as platinum and palladium, used in catalytic converters in automobiles, exemplify this property. They accelerate the conversion of harmful pollutants into less harmful substances.

Colored Compounds: A Spectacle of Electronic Transitions

The vibrant colors of many transition metal compounds are a direct consequence of the electronic transitions within the d sublevel. When light shines on these compounds, electrons in the d orbitals can absorb photons and jump to higher energy d orbitals.

The energy difference between the d orbitals determines the wavelength of light absorbed, and the complementary color is what we perceive. For example, copper(II) sulfate solutions appear blue because they absorb red and yellow light.

The presence or absence of ligands (molecules or ions bound to the metal center) affects the energies of the d orbitals. This will affect the color of the complex. This dependence makes transition metal complexes valuable as pigments and dyes.

Bonding Behavior and Coordination Complexes

The d orbitals play a crucial role in the bonding behavior of transition metals, particularly in the formation of coordination complexes. These complexes consist of a central metal ion surrounded by ligands, which donate electron pairs to the metal center.

The d orbitals of the metal ion interact with the orbitals of the ligands, forming coordinate covalent bonds. The number and arrangement of ligands around the metal ion determine the geometry of the complex, which in turn affects its properties.

Crystal Field Theory and Ligand Field Theory offer sophisticated models for understanding the electronic structure and bonding in coordination complexes, further highlighting the importance of d orbitals in determining their behavior.

Applications in Materials Science and Catalysis

The unique properties of transition metals, rooted in their d sublevel configurations, have led to a wide range of applications in materials science and catalysis.

In materials science, transition metals are used to create alloys with enhanced strength, corrosion resistance, and magnetic properties. The ability to fine-tune the electronic structure of these materials through alloying is crucial for optimizing their performance.

In catalysis, transition metal complexes are used as homogeneous catalysts in various industrial processes, including polymerization, oxidation, and hydrogenation. These catalysts offer high selectivity and activity, enabling the efficient synthesis of a wide range of chemical products.

Electron Density and Materials Characterization

Understanding the electron density distribution within materials containing transition metals is crucial for characterizing their properties. Techniques like X-ray diffraction and electron microscopy provide information about the arrangement of atoms and the distribution of electrons within the material.

This knowledge is essential for designing new materials with specific properties and for optimizing the performance of existing materials. Computational methods, such as density functional theory (DFT), are also used to model the electronic structure of materials and predict their behavior.

Video: Unlock the d Sublevel! How Many Orbitals Exist?! ⚛️

Play Video