Lennard-Jones Potential Explained: The Ultimate Guide!

The Lennard-Jones potential, a crucial concept in molecular dynamics simulations, accurately models the interaction energy between neutral atoms and molecules. Specifically, van der Waals forces, a manifestation of this potential, are critical for understanding phenomena such as protein folding. Research institutions like MIT extensively utilize the Lennard-Jones potential in computational chemistry for predicting material properties. Parameters used within the Lennard-Jones potential are often optimized through comparisons with experimental data obtained by researchers using the atomic force microscopy. Understanding the depth of the potential well, denoted as ε (epsilon), is vital when describing the attractive or repulsive interaction and in the study of condensed phases of matter with applications to the work of Johannes Diderik van der Waals who the force is named after.

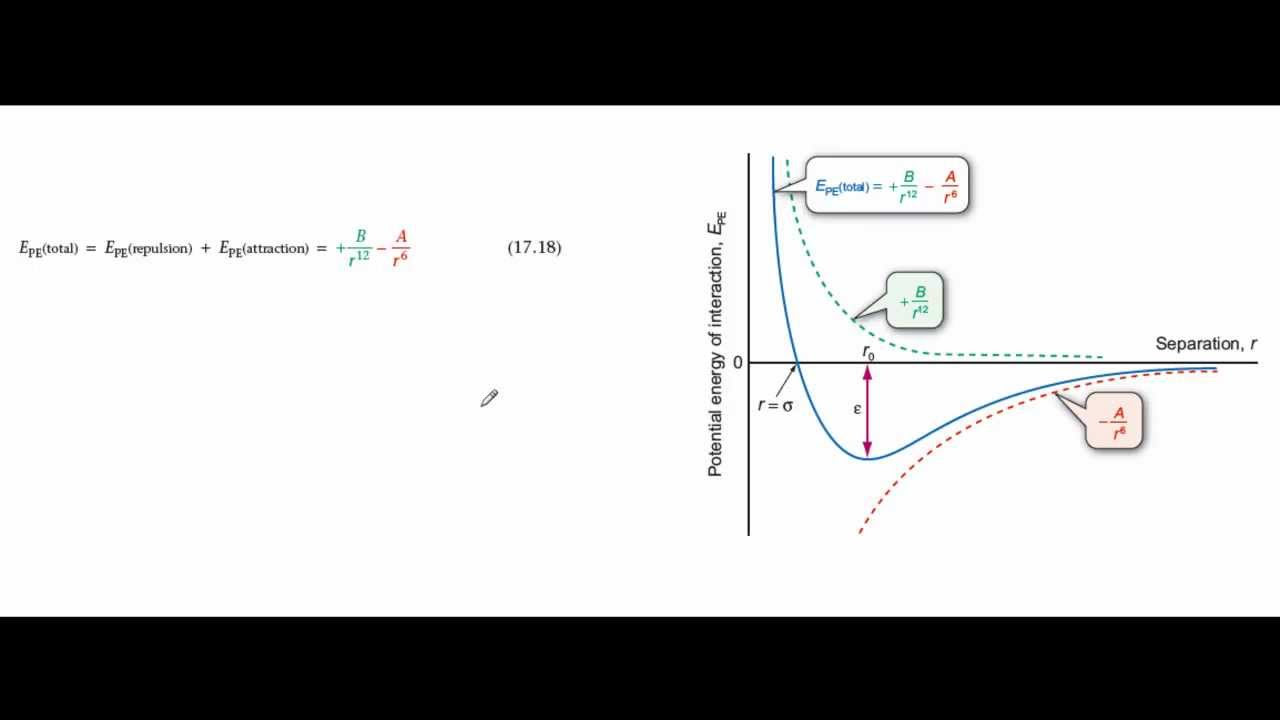
Image taken from the YouTube channel Oxford Academic (Oxford University Press) , from the video titled Molecular interaction and the Lennard-Jones potential .

The world around us, from the air we breathe to the materials that shape our lives, is governed by a delicate dance of attraction and repulsion between molecules. These interactions, collectively known as intermolecular forces, are the unsung heroes behind a vast array of phenomena.

Understanding these forces unlocks insights into diverse fields, ranging from the intricacies of biological systems to the design of novel materials with tailored properties.

The Ubiquitous Nature of Intermolecular Forces

Intermolecular forces are not confined to a specific domain of science. Their influence permeates various disciplines:

• Chemistry: They dictate the physical properties of substances, such as boiling points, melting points, and solubility.

• Biology: They are essential for protein folding, DNA structure, and enzyme-substrate interactions.

• Materials Science: They govern the adhesion, cohesion, and mechanical strength of materials.

• Pharmaceutical Science: Drug design relies heavily on understanding how drug molecules interact with biological targets through intermolecular forces.

From the condensation of water vapor to the self-assembly of complex biomolecules, intermolecular forces are the invisible architects shaping the world at the molecular level.

The Lennard-Jones Potential: A Cornerstone of Understanding

This article delves into one of the most fundamental and widely used models for describing intermolecular interactions: the Lennard-Jones potential.

This potential provides a simplified yet powerful representation of the forces between neutral atoms and molecules, capturing the essential balance between attractive and repulsive interactions.

We will explore its mathematical formulation, dissect the physical significance of its components, and examine its applications in various simulation techniques.

Ultimately, this article aims to provide a comprehensive understanding of the Lennard-Jones potential. We will cover the model's mathematical formulation, physical significance, and wide range of applications across scientific domains. By the end of this exploration, you will gain a deeper appreciation for the crucial role it plays in unraveling the mysteries of the molecular world.

The world around us, from the air we breathe to the materials that shape our lives, is governed by a delicate dance of attraction and repulsion between molecules. These interactions, collectively known as intermolecular forces, are the unsung heroes behind a vast array of phenomena.

Understanding these forces unlocks insights into diverse fields, ranging from the intricacies of biological systems to the design of novel materials with tailored properties.

Foundations: Delving into Intermolecular Forces

Before we can fully appreciate the elegance and utility of the Lennard-Jones potential, it’s essential to lay a firm groundwork in the fundamental principles governing interactions between molecules. This involves understanding the nature and origins of intermolecular forces, with a particular focus on Van der Waals forces and the crucial interplay between attractive and repulsive components.

Defining Intermolecular Forces

Intermolecular forces (IMFs) are the attractive or repulsive forces that mediate interactions between molecules, including atoms and ions. These forces are electrostatic, meaning they arise from the interaction of positive and negative charges. However, unlike the strong intramolecular forces (e.g., covalent bonds) that hold atoms together within a molecule, IMFs are significantly weaker.

The origin of IMFs lies in the distribution of electrons within molecules. Even in molecules with no net dipole moment, temporary fluctuations in electron density can create transient dipoles, leading to intermolecular interactions.

Van der Waals Forces

Van der Waals forces are a subset of intermolecular forces that include dipole-dipole, dipole-induced dipole, and London dispersion forces. These forces are ubiquitous and play a critical role in determining the physical properties of substances.

Understanding Van der Waals forces is paramount because they are the very foundation upon which the Lennard-Jones potential is built. They represent the dominant attractive forces that the Lennard-Jones potential seeks to model.

Types of Van der Waals Forces

• Keesom Forces (Dipole-Dipole): These forces occur between polar molecules, which possess permanent dipole moments. The positive end of one molecule is attracted to the negative end of another. The strength of the Keesom force depends on the magnitude of the dipole moments and the distance between the molecules.
• Debye Forces (Dipole-Induced Dipole): A polar molecule can induce a temporary dipole moment in a nonpolar molecule, leading to an attractive interaction. The strength of the Debye force depends on the magnitude of the dipole moment of the polar molecule and the polarizability of the nonpolar molecule.
• London Dispersion Forces (Instantaneous Dipole-Induced Dipole): These forces are present between all molecules, including nonpolar molecules. They arise from temporary fluctuations in electron density, creating instantaneous dipoles that induce dipoles in neighboring molecules. Although individually weak, London dispersion forces can be significant, especially for large molecules with many electrons.

Attractive Forces and Repulsive Forces

Intermolecular interactions are not solely governed by attractive forces. Repulsive forces also play a crucial role. These forces arise from the Pauli exclusion principle, which prevents electrons with the same spin from occupying the same region of space.

As molecules approach each other, their electron clouds begin to overlap, leading to a strong repulsive force.

The interplay between attractive and repulsive forces determines the equilibrium separation distance between molecules. At large distances, attractive forces dominate. As the distance decreases, the attractive forces increase until the electron clouds begin to overlap. At very short distances, the repulsive forces become dominant, preventing the molecules from collapsing into each other.

The Lennard-Jones potential elegantly captures this balance between long-range attraction and short-range repulsion, providing a simplified yet accurate representation of intermolecular interactions.

Van der Waals forces, as we’ve seen, provide the essential framework for understanding how molecules interact. However, to truly quantify and model these interactions, we need a mathematical tool that captures the balance between attraction and repulsion. Enter the Lennard-Jones potential, a remarkably elegant and widely used model that has become a cornerstone of molecular simulations and theoretical chemistry.

The Lennard-Jones Potential: A Detailed Exploration

The Lennard-Jones potential provides a mathematical model that approximates the interaction between a pair of neutral atoms or molecules. It's a simple yet powerful equation that captures the essence of intermolecular forces, balancing attractive and repulsive forces to predict the potential energy of a system as a function of the distance between particles.

The Visionary: Honouring John Lennard-Jones

The Lennard-Jones potential is named in honor of Sir John Edward Lennard-Jones, a British theoretical physicist and mathematician.

Lennard-Jones made significant contributions to our understanding of intermolecular forces and the structure of molecules. His pioneering work laid the foundation for modern molecular dynamics simulations and continues to influence research in various fields.

The Mathematical Formulation

The Lennard-Jones potential is mathematically expressed as:

V(r) = 4ε [(σ/r)¹² - (σ/r)⁶]

This equation might appear daunting at first glance, but its components are relatively straightforward to understand. Let's break it down:

• V(r): Represents the potential energy between two particles as a function of the distance, r.

• r: Is the distance between the centers of the two interacting particles (atoms or molecules).

• σ (Sigma): Is the collision diameter. It represents the distance at which the potential energy is zero. It essentially signifies the distance at which the repulsive and attractive forces balance each other.

• ε (Epsilon): Represents the well depth. It determines the depth of the potential well and corresponds to the strength of the attraction between the particles. It is the minimum potential energy.

Understanding the Components

The Lennard-Jones potential elegantly combines two terms, each representing a distinct aspect of intermolecular interaction: repulsion and attraction.

Short-Range Repulsion

The first term, (σ/r)¹², describes the repulsive force that arises when the electron clouds of two atoms or molecules begin to overlap. This repulsion is a consequence of the Pauli exclusion principle, which dictates that no two electrons can occupy the same quantum state.

As the distance r decreases, this term increases rapidly, leading to a strong repulsive force at short distances. This is also known as Pauli Repulsion. The exponent of 12 is chosen for computational convenience and provides a steep repulsive potential.

Long-Range Attraction

The second term, (σ/r)⁶, describes the attractive force due to London dispersion forces. These forces arise from temporary fluctuations in electron density, which induce dipoles in neighboring atoms or molecules.

As the distance r increases, this term decreases more gradually, representing a weaker, long-range attraction.

These London dispersion forces are present between all atoms and molecules, regardless of their polarity.

Potential Energy and Distance

The Lennard-Jones potential describes the relationship between the distance separating two particles and the potential energy between them.

At large distances, the potential energy approaches zero, indicating negligible interaction. As the particles approach each other, the attractive force dominates, causing the potential energy to decrease, reaching a minimum at an equilibrium distance.

At even shorter distances, the repulsive force becomes dominant, causing the potential energy to increase sharply.

Visualizing the Potential

The Lennard-Jones potential is often visualized as a curve plotting potential energy (V(r)) as a function of interparticle distance (r).

Interpreting the Potential Energy Curve

The shape of the curve provides valuable information about the interaction between the particles.

The x-axis represents the distance r between the two particles, and the y-axis represents the potential energy V(r).

The minimum of the curve represents the most stable separation distance between the two particles.

Potential Wells

The potential well is the region around the minimum of the curve. It represents the range of distances where the attractive forces dominate.

The depth of the potential well (ε) corresponds to the strength of the interaction: a deeper well indicates a stronger attraction. Particles tend to reside at the bottom of this well, representing their most stable configuration.

Understanding the depth and shape of the potential well is crucial for predicting the behavior of systems.

Van der Waals forces, as we’ve seen, provide the essential framework for understanding how molecules interact. However, to truly quantify and model these interactions, we need a mathematical tool that captures the balance between attraction and repulsion. Enter the Lennard-Jones potential, a remarkably elegant and widely used model that has become a cornerstone of molecular simulations and theoretical chemistry.

Decoding the Parameters: Sigma (σ) and Epsilon (ε)

The Lennard-Jones potential's power resides not only in its mathematical form, but also in the physical significance of its parameters. Two parameters, sigma (σ) and epsilon (ε), dictate the behavior of the interaction: the collision diameter and the well depth. Understanding these parameters is crucial for interpreting and applying the Lennard-Jones potential effectively.

Sigma (σ) – The Collision Diameter

The collision diameter, denoted by the Greek letter sigma (σ), is a fundamental parameter within the Lennard-Jones potential. It represents the distance at which the potential energy between two interacting particles is zero.

In simpler terms, it's the separation at which the attractive and repulsive forces are perfectly balanced, resulting in no net interaction energy.

Physical Significance of Sigma

Imagine two particles approaching each other. As they get closer, they initially experience attractive forces. At very short ranges, repulsive forces begin to dominate. The collision diameter (σ) marks the point where these forces precisely cancel each other out.

This distance is closely related to the size of the interacting particles. A larger particle will naturally have a larger collision diameter. The value of σ provides an estimate of the effective "hard sphere" radius of the atom or molecule.

It's essential to note that σ doesn't represent the actual physical size of the atom or molecule in the traditional sense. Instead, it represents the effective distance at which the repulsive forces become significant enough to prevent further approach.

Epsilon (ε) – The Well Depth

The well depth, denoted by the Greek letter epsilon (ε), is another critical parameter in the Lennard-Jones potential. It represents the depth of the potential well, which corresponds to the minimum potential energy of the system.

Interpreting Epsilon: Interaction Strength

Epsilon (ε) dictates the strength of the attractive interaction between the particles. A larger value of ε indicates a stronger attraction, meaning more energy is required to separate the particles from their equilibrium distance.

The well depth corresponds to the most stable configuration, where the attractive and repulsive forces are optimally balanced, resulting in the lowest possible potential energy.

Epsilon and Separation Energy

The magnitude of epsilon (ε) directly relates to the energy needed to completely separate the two interacting particles from their equilibrium distance.

A system with a deeper potential well (larger ε) requires more energy to overcome the attractive forces and move the particles infinitely far apart. Conversely, a shallow potential well (smaller ε) indicates a weaker interaction, and less energy is needed for separation.

r (distance) - The Distance Between Two Atoms/Molecules

In the context of the Lennard-Jones potential, "r" represents the distance between the centers of the two interacting atoms or molecules. It's the variable upon which the potential energy, V(r), depends. As 'r' changes, the balance between attractive and repulsive forces shifts, causing the potential energy to vary.

The Lennard-Jones potential calculates the interaction energy as a function of this distance, allowing us to model how the forces change as atoms or molecules move closer or further apart.

Factors Affecting Sigma (σ) and Epsilon (ε)

The values of sigma (σ) and epsilon (ε) are not universal constants. They are specific to the type of atoms or molecules involved and are influenced by several factors:

• Atomic/Molecular Size: Larger atoms and molecules generally exhibit larger collision diameters (σ) due to their increased electron cloud size.
• Polarizability: The ease with which the electron cloud of an atom or molecule can be distorted influences the strength of the London dispersion forces, impacting the well depth (ε).
• Electronic Structure: The electronic configuration of the atoms or molecules affects their ability to interact, influencing both σ and ε.
• Chemical Composition: Different chemical elements and molecular structures exhibit different intermolecular interactions, leading to variations in σ and ε.
• Temperature: While the Lennard-Jones parameters themselves are typically considered temperature-independent, the effective interaction between particles can be influenced by temperature through changes in kinetic energy and average separation distances.

Understanding these influencing factors is critical for selecting appropriate values for sigma (σ) and epsilon (ε) when modeling real-world systems. Accurate parameterization is key to obtaining reliable simulation results.

Van der Waals forces, as we’ve seen, provide the essential framework for understanding how molecules interact. However, to truly quantify and model these interactions, we need a mathematical tool that captures the balance between attraction and repulsion. Enter the Lennard-Jones potential, a remarkably elegant and widely used model that has become a cornerstone of molecular simulations and theoretical chemistry. With a firm grasp on the potential’s parameters, let's now explore its real-world applications and how it empowers researchers to investigate complex systems.

Applications in Action: Leveraging the Lennard-Jones Potential

The Lennard-Jones potential transcends theoretical elegance; it's a practical tool extensively used in various computational techniques to simulate and understand the behavior of matter at the molecular level. Its simplicity and computational efficiency make it invaluable in fields ranging from materials science to biophysics. Let's delve into some key applications.

Molecular Dynamics Simulations: A Microscopic View of the World

Molecular dynamics (MD) simulations are arguably the most prominent application of the Lennard-Jones potential. In essence, MD simulations involve solving Newton's equations of motion for a system of interacting particles over time.

The Lennard-Jones potential provides the force field that governs the interactions between these particles, dictating how they attract and repel each other as a function of distance.

Modeling Interatomic and Intermolecular Interactions

In MD simulations, the Lennard-Jones potential acts as a simplified, yet effective, representation of the complex interactions between atoms and molecules.

By calculating the forces arising from this potential, researchers can predict the trajectory of each particle in the system, providing a dynamic picture of its evolution.

Simulating Liquids, Gases, and Solids

One of the remarkable strengths of the Lennard-Jones potential lies in its ability to simulate the behavior of matter in different phases.

• Liquids: MD simulations using the Lennard-Jones potential can accurately reproduce the structural and dynamic properties of simple liquids, such as diffusion coefficients and radial distribution functions.

• Gases: The potential is also suitable for modeling the behavior of gases, particularly at moderate densities where intermolecular interactions are significant.

• Solids: In the case of solids, the Lennard-Jones potential can be used to investigate phenomena such as crystal structure, thermal expansion, and mechanical properties.

Beyond Molecular Dynamics: Other Simulation Techniques

While MD simulations are the primary application, the Lennard-Jones potential also finds use in other computational methods:

• Monte Carlo Simulations: The Lennard-Jones potential can be incorporated into Monte Carlo simulations, which are statistical methods used to sample the configuration space of a system. This allows researchers to calculate thermodynamic properties, such as energy and pressure.

• Brownian Dynamics: For systems where the solvent plays a significant role, Brownian dynamics simulations can be employed. The Lennard-Jones potential is used to model the interactions between solute particles, while the effect of the solvent is treated as a stochastic force.

Empirical Potentials: Building Blocks for Complex Force Fields

The Lennard-Jones potential serves as a fundamental building block for more sophisticated empirical potentials, also known as force fields. These force fields are designed to model a wider range of chemical systems, including complex molecules and biomolecules.

The Foundation of Force Fields

Force fields typically include terms for bond stretching, angle bending, and torsional rotations, in addition to non-bonded interactions. The non-bonded interactions are often modeled using a combination of the Lennard-Jones potential for van der Waals forces and Coulomb's law for electrostatic interactions.

Parameterization and Refinement

Developing accurate force fields is a challenging task that involves carefully parameterizing the potential energy functions based on experimental data and quantum mechanical calculations.

The Lennard-Jones parameters (σ and ε) are often adjusted to reproduce the observed properties of the system, such as density, heat of vaporization, and crystal structure.

By combining the Lennard-Jones potential with other energy terms, researchers can create force fields that provide a realistic and computationally efficient description of complex molecular systems, enabling simulations of unprecedented scale and complexity.

Van der Waals forces, as we’ve seen, provide the essential framework for understanding how molecules interact. However, to truly quantify and model these interactions, we need a mathematical tool that captures the balance between attraction and repulsion. Enter the Lennard-Jones potential, a remarkably elegant and widely used model that has become a cornerstone of molecular simulations and theoretical chemistry. With a firm grasp on the potential’s parameters, let's now explore its real-world applications and how it empowers researchers to investigate complex systems.

Limitations and Alternatives: Knowing the Boundaries

While the Lennard-Jones potential provides a remarkably versatile and computationally efficient method for approximating intermolecular interactions, it's crucial to recognize its inherent limitations. No single model can perfectly capture the complexities of all molecular systems, and the Lennard-Jones potential is no exception. Understanding these boundaries is essential for choosing the right tool for the job and interpreting simulation results with appropriate caution.

Inherent Simplifications of the Lennard-Jones Potential

The very features that make the Lennard-Jones potential so useful—its simplicity and computational efficiency—also contribute to its limitations. The potential relies on a spherically symmetric approximation, treating atoms and molecules as point particles interacting via central forces.

This simplification neglects the directional nature of many chemical bonds and interactions, such as hydrogen bonds and covalent bonds. Moreover, the fixed exponents in the repulsive (r^-12) and attractive (r^-6) terms are not universally applicable and can lead to inaccuracies in certain systems.

Challenges in Modeling Specific Interactions

Several types of interactions are poorly represented by the standard Lennard-Jones potential:

• Electrostatic Interactions: The Lennard-Jones potential is inherently non-polar. It does not explicitly account for electrostatic interactions arising from partial charges or dipoles within molecules. Systems with significant electrostatic contributions, such as ionic compounds or highly polar molecules in solution, require more sophisticated models that incorporate Coulombic terms.

• Covalent Bonding: The Lennard-Jones potential is designed to model non-bonded interactions. It cannot describe the formation or breaking of covalent bonds, which involve significant electronic rearrangements. Simulating chemical reactions or systems with dynamic bonding requires reactive force fields or quantum mechanical methods.

• Hydrogen Bonding: While sometimes approximated by adjusted Lennard-Jones parameters, hydrogen bonds possess a strong directional character that is not well-captured by the spherically symmetric potential. Specialized hydrogen bonding potentials are often necessary for accurate simulations of systems where these interactions play a crucial role (e.g., water, proteins).

Exploring Alternative Potentials

When the limitations of the Lennard-Jones potential become significant, a range of alternative potential functions offers improved accuracy at the cost of increased computational complexity. Here are a few examples:

• Morse Potential: The Morse potential provides a more realistic description of diatomic bond stretching compared to the harmonic potential often used in simple force fields. It accounts for bond dissociation at large distances, which is essential for modeling molecular vibrations and reactions.

• Buckingham Potential: Similar to the Lennard-Jones potential, the Buckingham potential describes non-bonded interactions but uses an exponential term for repulsion instead of the r^-12 term. This exponential repulsion can provide a more accurate representation of the electron cloud overlap at short distances, particularly for ionic systems.

• Embedded Atom Model (EAM): EAM potentials are often used to simulate metallic systems, where the electronic structure is more complex than can be captured by simple pair potentials. EAM potentials consider the local electronic environment of each atom, providing a more accurate description of bonding and mechanical properties.

• Ab Initio (Quantum Mechanical) Methods: For the highest accuracy, particularly when dealing with chemical reactions or complex electronic structures, ab initio quantum mechanical methods can be employed. These methods solve the Schrödinger equation directly, without relying on empirical parameters. However, they are computationally demanding and typically limited to smaller systems or shorter simulation times.

It is important to note that the choice of potential function depends heavily on the specific system and the desired level of accuracy. While alternative potentials can address some of the limitations of the Lennard-Jones potential, they often come with increased computational cost and complexity. The Lennard-Jones potential remains a valuable tool for many applications due to its balance of accuracy and efficiency, but it is crucial to be aware of its limitations and consider alternative approaches when necessary.

While the Lennard-Jones potential provides a remarkably versatile and computationally efficient method for approximating intermolecular interactions, it's crucial to recognize its inherent limitations. No single model can perfectly capture the complexities of all molecular systems, and the Lennard-Jones potential is no exception. Understanding these boundaries is essential for choosing the right tool for the job and interpreting simulation results with appropriate caution.

Behind every groundbreaking scientific achievement, there are often pioneers whose work laid the very foundation upon which new theories and models are built. In the context of intermolecular forces and the Lennard-Jones potential, that pioneer is undoubtedly Johannes Diderik van der Waals. His insights into the behavior of real gases and the nature of intermolecular interactions were revolutionary, paving the way for more sophisticated models like the Lennard-Jones potential to emerge.

A Historical Perspective: The Legacy of Van der Waals

Johannes Diderik van der Waals, a Dutch theoretical physicist, stands as a monumental figure in the history of molecular physics. His work in the late 19th century dramatically shifted our understanding of gases and liquids, moving beyond the idealized models that had previously dominated the field.

Van der Waals' most significant contribution was recognizing that real gases deviate from the ideal gas law due to two crucial factors: the finite volume of gas molecules and the presence of attractive forces between them.

Van der Waals' Equation of State: A Step Beyond Ideality

The ideal gas law, PV = nRT, provides a simple and elegant description of gas behavior under certain conditions. However, it assumes that gas molecules are point masses with no volume and that there are no interactions between them.

Van der Waals realized that these assumptions were unrealistic. To account for the volume occupied by gas molecules, he introduced a correction term, 'b', to the volume term in the ideal gas law. This term represents the excluded volume per mole of gas, effectively reducing the available space for molecular motion.

He also introduced a correction term, 'a', to account for the attractive forces between gas molecules. These forces, now known as Van der Waals forces, reduce the pressure exerted by the gas on the container walls.

The resulting Van der Waals equation of state is:

(P + a(n/V)²)(V - nb) = nRT

This equation provides a much more accurate description of real gas behavior than the ideal gas law, particularly at high pressures and low temperatures where intermolecular forces become significant.

The Significance of Intermolecular Forces

Van der Waals' recognition of intermolecular forces was a paradigm shift. He understood that these forces, though weaker than chemical bonds, play a crucial role in determining the physical properties of matter, including:

• Boiling points and melting points
• Surface tension
• Viscosity
• Phase transitions

His work demonstrated that molecules are not simply inert particles but are capable of interacting with each other, leading to a richer and more complex understanding of matter.

The Foundation for Lennard-Jones

While Van der Waals did not explicitly define the mathematical form of the potential energy function describing these intermolecular forces, his conceptual framework was essential for the development of models like the Lennard-Jones potential.

The Lennard-Jones potential builds upon Van der Waals' ideas by providing a specific mathematical description of the balance between attractive and repulsive forces.

The r^-6 attractive term in the Lennard-Jones potential is directly related to the London dispersion forces, a type of Van der Waals force. The repulsive term, r^-12, represents the short-range repulsion that arises when molecules get too close, an effect also implicitly recognized by Van der Waals through the finite volume correction in his equation of state.

In essence, the Lennard-Jones potential can be viewed as a quantitative refinement of Van der Waals' qualitative insights. It takes the fundamental concepts introduced by Van der Waals and translates them into a mathematical form that can be used for quantitative calculations and simulations.

A Lasting Impact

Johannes Diderik van der Waals' legacy extends far beyond the equation that bears his name. His pioneering work on intermolecular forces laid the foundation for a vast field of research, influencing areas such as:

• Molecular dynamics simulations
• Materials science
• Chemical engineering
• Drug discovery

His insights continue to inspire scientists and engineers today, reminding us of the power of fundamental understanding in unlocking the secrets of the molecular world. Without Van der Waals' groundwork, the Lennard-Jones potential, with its power to model and predict molecular interactions, would likely not exist in its current form.

Video: Lennard-Jones Potential Explained: The Ultimate Guide!

Play Video