Cone's Lateral Area: Simple Formulas You Need to Know!
The concept of surface area, foundational in geometry, directly relates to understanding the lateral area of a cone. This measurement, critical for calculations in fields like engineering, depends significantly on the cone's slant height. Numerous online calculators are available to aid in these calculations, although a solid grasp of the underlying formulas is essential for accurate application. Understanding the lateral area of a cone, therefore, allows for precise assessments of conical surfaces.
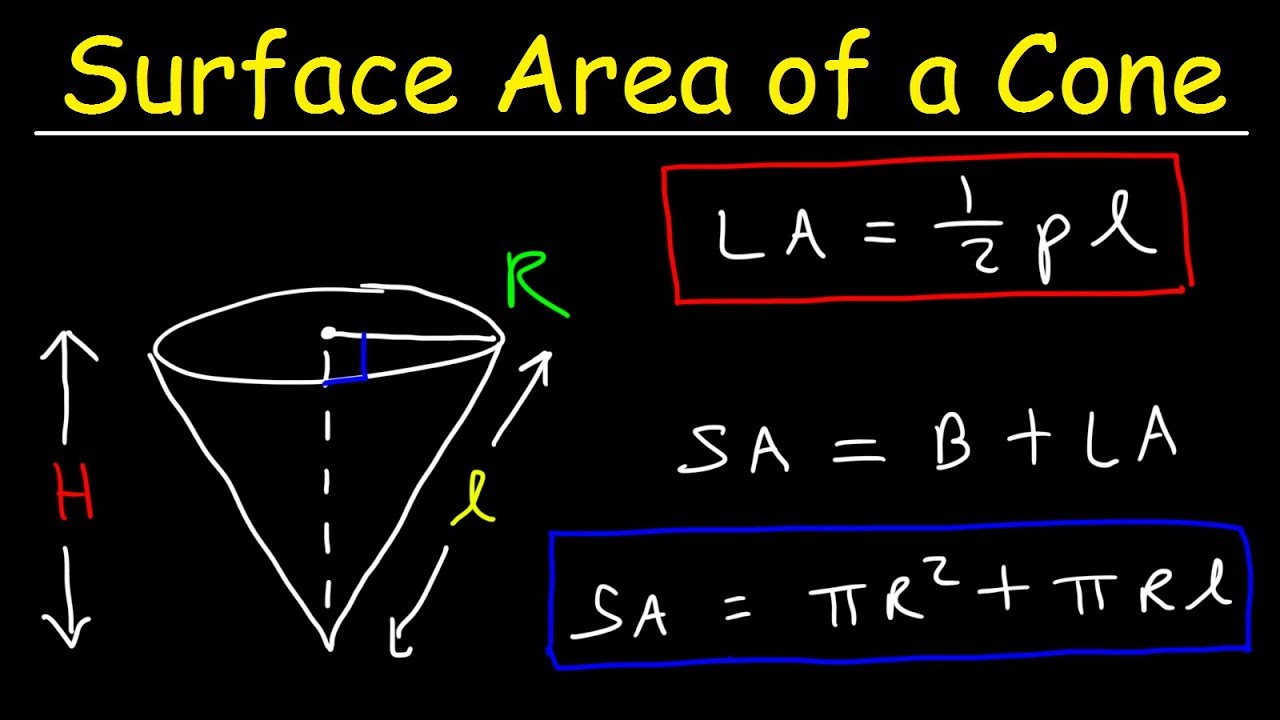
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Surface Area of a Cone with Lateral Area - geometry .
The world around us is filled with geometric shapes, some more obvious than others. Among these, the cone stands out with its distinctive form, appearing everywhere from ice cream treats to architectural marvels. This section serves as your gateway to understanding the cone and, more specifically, its lateral area.
We'll explore what lateral area represents and why it's a crucial measurement in various practical applications.
Defining the Cone: A Geometric Overview
At its core, a cone is a three-dimensional geometric shape that tapers smoothly from a flat base (typically circular) to a point called the apex or vertex. Key components define its structure:
- Base: The circular bottom of the cone.
- Apex: The point at the top, opposite the base.
- Height: The perpendicular distance from the apex to the center of the base.
- Slant Height: The distance from the apex to any point on the edge of the base.
- Radius: The distance from the center of the base to its edge.
Understanding these elements is foundational to grasping the concept of lateral area.
Why Lateral Area Matters: Real-World Relevance
The lateral area of a cone refers to the area of its curved surface, excluding the base. Why is this important? Consider these scenarios:
- Manufacturing: Calculating the material needed to produce conical containers or funnels.
- Construction: Determining the surface area of a conical roof.
- Design: Estimating the fabric required for a lampshade.
In each of these cases, knowing the lateral area allows for accurate material estimation, cost efficiency, and effective design implementation.
A Captivating Hook: The Great Pyramid's Hidden Cones
Did you know that the Great Pyramid of Giza, while primarily a pyramid, also implicitly embodies conical properties? While not a perfect cone, its structure shares geometric principles, and understanding surface area calculations is essential in analyzing such monumental constructions. Exploring the lateral area of cones, therefore, connects us to both everyday applications and historical wonders, sparking curiosity and highlighting the practical significance of this geometric concept.
The cone, with its sloping side culminating in a sharp apex, has its share of practical uses. But, to truly utilize the geometric properties of a cone effectively, one must understand the concept of lateral area. This understanding becomes the key to unlocking accurate calculations and efficient designs involving conical forms.
Demystifying Lateral Area: What It Really Means
Lateral area is a specific measurement that focuses on a particular part of a three-dimensional object. Unlike other area measurements, the lateral area hones in on the curved surface of a cone, excluding its base. It represents the extent of the cone's side, essentially the area you would need to cover if you were wrapping the cone like a gift, leaving the circular bottom exposed.
Defining Lateral Area in the Context of a Cone
In the context of a cone, the lateral area is defined as the area of the curved surface extending from the base to the apex, not including the area of the base itself. Imagine unrolling the cone's side – it would form a sector of a circle. The area of this sector is what we refer to as the lateral area.
Lateral Area vs. Total Surface Area: Knowing the Difference
It's crucial to differentiate lateral area from total surface area. While the lateral area considers only the curved side, the total surface area encompasses both the lateral area and the area of the base.
Therefore:
Total Surface Area = Lateral Area + Base Area
This distinction is vital in practical applications. If you're calculating the amount of material needed to construct a conical roof, you might only need the lateral area. However, if you're determining the amount of paint required to cover the entire cone, including the bottom, you'll need to calculate the total surface area.
The Role of Geometry
Geometry provides the framework for understanding the spatial properties of the cone and, consequently, its lateral area. Geometric principles allow us to define the cone's dimensions, such as its radius, height, and slant height, which are all essential in calculating the lateral area.
Furthermore, geometry helps us visualize the cone in different ways, such as understanding how the lateral area can be "unrolled" into a flat sector of a circle. This visualization is fundamental in grasping the concept of lateral area and its calculation.
Visualizing Lateral Area
[Insert a visual aid here: A diagram of a cone with the lateral area clearly highlighted (perhaps shaded or labeled). The base should be distinct, indicating that it's not part of the lateral area. Consider also including an "unrolled" representation of the cone's lateral surface as a sector of a circle.]
A visual aid provides an intuitive understanding of what the lateral area represents. It helps to solidify the concept in the reader's mind, making it easier to remember and apply in practical scenarios. By seeing the lateral area as a distinct part of the cone's surface, readers can avoid confusing it with the total surface area and improve their problem-solving accuracy.
The Magic Formula: Decoding the Lateral Area Equation
Having established what lateral area signifies in the context of a cone, it's time to introduce the formula that allows us to calculate it. This formula is the key to unlocking a world of practical applications, from engineering designs to everyday problem-solving.
Unveiling the Formula: πrl
The lateral area of a cone is calculated using a remarkably simple and elegant formula:
Lateral Area = π Radius Slant Height, often written as πrl.
This formula states that the lateral area is the product of three key values: pi, the radius of the cone's base, and the slant height of the cone.
Let's break down each of these components to understand how they contribute to the overall calculation.
Decoding the Variables
Each symbol in the formula represents a specific measurement of the cone. Understanding these measurements is crucial for accurate calculation and application.
Pi (π): The Unchanging Constant
Pi (π) is a mathematical constant representing the ratio of a circle's circumference to its diameter. This value is approximately 3.14159, although for many practical calculations, using 3.14 is sufficient.
It's a universal constant, meaning its value remains the same regardless of the size of the circle or, in this case, the cone's base.
Radius (r): The Circle's Span
The radius (r) is the distance from the center of the circular base of the cone to any point on the edge of that base.
It is a fundamental measurement that defines the size of the cone's base and directly impacts its lateral area.
Ensure you're measuring from the center of the circle for an accurate radius value.
Slant Height (l): The Cone's Slope
The slant height (l) is the distance from the apex (the tip) of the cone to any point on the edge of the circular base.
It is not the same as the regular height of the cone, which is the perpendicular distance from the apex to the center of the base. The slant height is always longer than the regular height (except in the theoretical case of a cone with zero height, which would essentially be a flat circle).
Visualizing the slant height as the length of a line tracing the cone's surface from the apex to the base is helpful.
Height, Slant Height, and Radius: A Geometric Relationship
While the slant height is directly used in the lateral area formula, the cone's regular height (h) plays an important role in determining the slant height itself, especially when it isn't directly provided.
The height, slant height, and radius of a cone form a right triangle. This relationship is critical, as it allows us to calculate the slant height using the Pythagorean theorem when only the height and radius are known. This will be explored in detail in the next section.
Finding the Slant Height: Unleashing the Power of the Pythagorean Theorem
Understanding the relationship between a cone's dimensions is key to unlocking its secrets. While the lateral area formula, πrl, requires the slant height (l), it's not always directly provided. Fear not, because the Pythagorean theorem provides a powerful tool to calculate the slant height when only the radius (r) and regular height (h) are known.
The Cone as a Right Triangle
The magic lies in recognizing the right triangle nestled within the cone. Imagine slicing the cone vertically through its apex and the center of its base. This cross-section reveals a triangle where:
-
The height of the cone (h) forms one leg.
-
The radius of the base (r) forms the other leg.
-
The slant height (l) acts as the hypotenuse.
This geometric insight allows us to apply the well-known Pythagorean theorem.
The Pythagorean Theorem: A Refresher
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematically, this is expressed as: a² + b² = c², where 'c' is the hypotenuse and 'a' and 'b' are the other two sides.
Applying the Theorem to Find Slant Height
In the context of our cone, we can rewrite the Pythagorean Theorem to solve for the slant height (l):
l² = r² + h²
To isolate 'l', we take the square root of both sides:
Slant Height = √(Radius² + Height²) or l = √(r² + h²)
This formula is your key to finding the slant height when the radius and height are known.
Visualizing the Relationship
A visual aid significantly enhances understanding. Imagine a diagram of the cone with the right triangle clearly highlighted. Label the height (h), radius (r), and slant height (l). This visual representation reinforces the connection between the cone's dimensions and the Pythagorean Theorem.
The radius and height meet at a right angle, forming the legs of the right triangle. The slant height, connecting the apex to the edge of the base, completes the triangle as the hypotenuse.
A Practical Example
Let's say you have a cone with a radius of 3 cm and a height of 4 cm. To find the slant height:
- Square the radius: 3² = 9
- Square the height: 4² = 16
- Add the squares: 9 + 16 = 25
- Take the square root: √25 = 5
Therefore, the slant height of the cone is 5 cm.
By understanding the relationship between the cone's dimensions and applying the Pythagorean Theorem, calculating the slant height becomes a straightforward process. This is a crucial step in determining the lateral area and unlocking further insights into the cone's geometry.
Finding the slant height equips you with the necessary tools, but true understanding comes from application. Let's solidify your knowledge by working through several step-by-step examples.
Step-by-Step Examples: Mastering the Calculation
This section will provide practical examples demonstrating the application of the lateral area formula and the slant height calculation using the Pythagorean theorem.
We'll explore scenarios where both the radius and slant height are provided, allowing for direct application of the lateral area formula.
Additionally, we'll tackle cases where only the radius and regular height are given, requiring you to first calculate the slant height.
Each example will be broken down step-by-step.
Example 1: Direct Application of the Lateral Area Formula
Let's start with a straightforward example.
Imagine a cone with a radius of 5 cm and a slant height of 12 cm. We want to find its lateral area.
Recall the formula: Lateral Area = πrl
- Identify the values: r = 5 cm, l = 12 cm.
- Substitute the values into the formula: Lateral Area = π 5 cm 12 cm.
- Calculate: Lateral Area = π
**60 cm².
- Approximate using π ≈ 3.14159: Lateral Area ≈ 3.14159** 60 cm².
- Final Answer: Lateral Area ≈ 188.5 cm².
Therefore, the lateral area of the cone is approximately 188.5 square centimeters.
Example 2: Calculating Slant Height First
Now, let's consider a slightly more complex scenario.
Suppose we have a cone with a radius of 8 inches and a regular height of 15 inches. Our goal is to determine its lateral area.
Notice that we don't have the slant height directly.
We need to use the Pythagorean Theorem to find it.
- Recall the Pythagorean Theorem: l² = r² + h².
- Identify the values: r = 8 inches, h = 15 inches.
- Substitute the values into the formula: l² = (8 inches)² + (15 inches)².
- Calculate: l² = 64 inches² + 225 inches².
- Simplify: l² = 289 inches².
- Take the square root of both sides: l = √(289 inches²).
- Solve for l: l = 17 inches.
Now that we have the slant height (l = 17 inches), we can calculate the lateral area using the formula: Lateral Area = πrl.
- Substitute the values: Lateral Area = π 8 inches 17 inches.
- Calculate: Lateral Area = π
**136 inches².
- Approximate using π ≈ 3.14159: Lateral Area ≈ 3.14159** 136 inches².
- Final Answer: Lateral Area ≈ 427.3 inches².
The lateral area of this cone is approximately 427.3 square inches.
Example 3: Working with a Right Cone
A right cone is simply a cone where the apex is directly above the center of the base. This doesn't change the formulas or calculations, but it's worth reinforcing.
Let’s consider a right cone with a radius of 6 meters and a slant height of 10 meters.
What is the lateral area?
- Identify the values: r = 6 meters, l = 10 meters.
- Apply the lateral area formula: Lateral Area = πrl = π 6 meters 10 meters.
- Calculate: Lateral Area = 60π square meters.
- Approximate: Lateral Area ≈ 60 * 3.14159 square meters ≈ 188.5 square meters.
Key Takeaways
- Always carefully identify the given values (radius, height, slant height).
- If the slant height is not provided, use the Pythagorean Theorem to calculate it.
- Remember the lateral area formula: Lateral Area = πrl.
- Pay attention to units and ensure consistency throughout your calculations.
By working through these examples, you've gained practical experience in calculating the lateral area of a cone. Practice with more examples to solidify your understanding and build confidence.
Finding the lateral area allows you to understand the surface of a cone, excluding its base. To truly master cone geometry, it's crucial to understand how this differs from the total surface area.
Lateral Area vs. Total Surface Area: Understanding the Difference
Let's revisit the lateral area and then see how it relates to the total surface area, which includes the base.
Lateral Area Revisited
Lateral area is the area of the curved surface of a cone, essentially the cone's "side". It's the part you would paint if you were only painting the sloping surface.
Recall the formula: Lateral Area = πrl, where:
- π (pi) is approximately 3.14159.
- r is the radius of the circular base.
- l is the slant height of the cone.
This formula gives you the area of the "wrapper" of the cone, without considering the bottom.
Total Surface Area: Including the Base
The total surface area encompasses the entire exterior surface of the cone. It includes both the lateral area (the curved surface) and the area of the circular base.
To calculate the total surface area, you simply add the area of the base to the lateral area. The area of the circular base is given by the formula πr².
Therefore, the formula for the total surface area of a cone is:
Total Surface Area = Lateral Area + Base Area = πrl + πr²
Visual Comparison
Imagine a paper cone, like one you'd get ice cream in. The lateral area is the amount of paper needed to make the cone itself, excluding the circular piece at the bottom.
The total surface area is the amount of paper needed to make the entire cone, including that circular bottom piece.
A diagram would clearly show the lateral area as the curved surface and the base as the circle at the bottom, highlighting the area included in the total surface area but excluded from the lateral area. This visual reinforces the difference between the two concepts.
Real-World Applications: Where Lateral Area Matters
Finding the lateral area allows you to understand the surface of a cone, excluding its base. To truly master cone geometry, it's crucial to understand how this differs from the total surface area.
But beyond abstract calculations, where does the concept of lateral area truly shine? The answer lies in its pervasive presence in various real-world applications. Understanding the lateral area of a cone unlocks possibilities in manufacturing, construction, design, and beyond.
Manufacturing: Optimizing Conical Containers
The manufacturing industry heavily relies on precise calculations for material usage. Consider conical containers: ice cream cones, funnels, or even certain types of packaging.
Calculating the lateral area is paramount in determining the amount of material needed to produce these items. Too little, and the container is incomplete; too much, and valuable resources are wasted.
By accurately calculating the lateral area, manufacturers can optimize material usage, reduce costs, and minimize waste, contributing to a more sustainable and efficient production process.
Construction: Engineering Sloped Roofs
Conical roofs, while aesthetically pleasing, require careful planning and execution. Determining the surface area of such a roof is vital for estimating the cost of roofing materials like shingles or tiles.
The lateral area calculation provides a precise estimate of the roof's surface, enabling builders to accurately order materials and avoid costly overages or shortages.
Furthermore, understanding the lateral area helps in assessing the roof's exposure to the elements, influencing decisions related to weatherproofing and structural integrity.
Design: Crafting Elegant Lampshades and Artistic Structures
Designers often employ cones in creating visually appealing objects, from lampshades to architectural features. Knowing the lateral area allows designers to calculate the amount of material needed to cover the conical surface.
Whether it's fabric for a lampshade or sheet metal for a sculpture, the lateral area provides a crucial metric for material selection and cost estimation. This knowledge is essential for bringing creative visions to life while staying within budget and resource constraints.
Specific Examples: Scenarios Where Lateral Area is Crucial
To further illustrate the importance of lateral area, consider these specific scenarios:
- Designing a Traffic Cone: Calculating the lateral area helps determine the amount of reflective material needed to ensure visibility and safety on roads.
- Creating a Teepee Tent: Estimating the lateral area is essential for calculating the amount of canvas required to construct the tent's conical walls.
- Building a Grain Silo: The lateral area calculation helps determine the surface area of the silo's conical roof, crucial for weatherproofing and structural integrity.
These examples demonstrate that the lateral area of a cone isn't just a theoretical concept, it's a practical tool that finds application in diverse fields, impacting design, efficiency, and cost-effectiveness.
Video: Cone's Lateral Area: Simple Formulas You Need to Know!
FAQs: Cone's Lateral Area Explained
Here are some common questions about understanding and calculating the lateral area of a cone.
What exactly is the lateral area of a cone?
The lateral area of a cone is the surface area of the cone, excluding the base. It's the area of the curved surface that connects the base to the vertex (or tip) of the cone.
What's the simplest formula for calculating the lateral area of a cone?
The easiest formula to use is πrl, where 'π' (pi) is approximately 3.14159, 'r' is the radius of the circular base, and 'l' is the slant height of the cone. This directly gives you the lateral area.
What if I only know the height and radius of the cone?
If you know the height (h) and radius (r), you can find the slant height (l) using the Pythagorean theorem: l = √(r² + h²). Then, plug the calculated slant height into the πrl formula to find the lateral area of a cone.
Why is understanding the lateral area of a cone important?
Understanding the lateral area is useful in various real-world applications, from calculating the material needed to construct a cone-shaped roof or a party hat to solving geometric problems involving three-dimensional shapes. It's a fundamental concept in geometry and calculus.
