Neon's Atomic Secrets: Bohr Model Explained!

Understanding the structure of atoms is fundamental in chemistry, and examining the bohr model of neon provides a crucial stepping stone. Niels Bohr's atomic model serves as the foundation, even with its limitations, for visualizing electron arrangements. The specific electron configuration of neon, a noble gas, results in its notable inertness. Quantum mechanics describes atomic behavior with more sophistication, but the Bohr model of neon offers a simplified, easily grasped explanation. Scientists and students often use the spectroscopic analysis of neon's emitted light to validate and refine their understanding of how the bohr model of neon relates to observed phenomena.

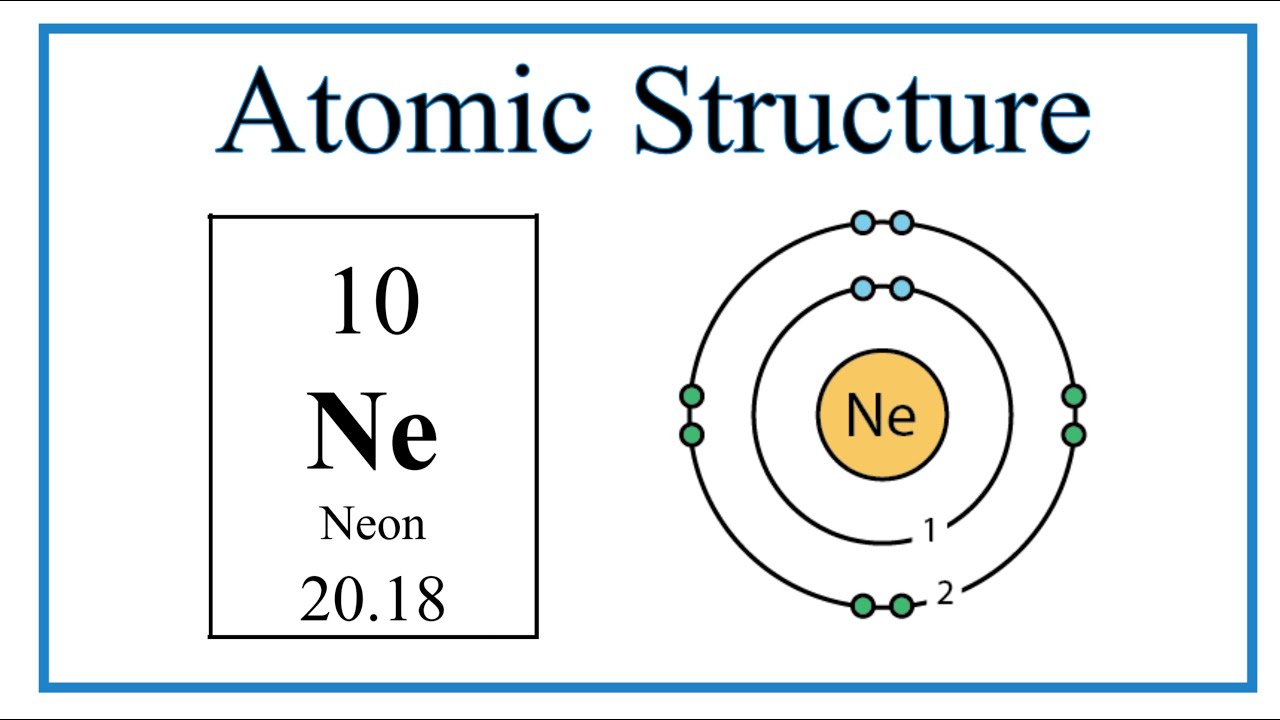
Image taken from the YouTube channel Wayne Breslyn (Dr. B.) , from the video titled Atomic Structure (Bohr Model) for the Neon (Ne) Atom .

Neon. The very name conjures images of vibrant cityscapes, buzzing storefronts, and retro signs that have become cultural icons. But beyond its artistic and commercial applications, neon (Ne) holds a deeper significance: it's a window into the fundamental laws governing the atomic world.

This seemingly simple element, responsible for those captivating glows, possesses a unique atomic structure that dictates its behavior. This structure, the key to understanding why neon lights up the way it does, is precisely what we aim to explore.

From Signs to Science: Unveiling Neon's Essence

Neon's most recognizable application is, of course, in neon signs. These signs, with their distinctive and varied colors (though pure neon glows a characteristic orange-red), have illuminated our world for over a century.

The bright glow we associate with neon signs arises from the element's unique ability to emit light when energized by an electrical current. But how does this happen? What is it about neon's atomic makeup that allows it to produce such a striking display?

Peering Inside the Atom: A Journey to the Core

The key to unlocking the mystery lies within the atom itself. To truly grasp neon's behavior, we must delve into the realm of atomic structure.

While modern physics offers highly sophisticated models of the atom, a foundational stepping stone to understanding neon's properties is the Bohr Model. Though not a perfect representation of atomic reality, the Bohr Model provides a clear and intuitive framework for understanding how electrons, and therefore light, interact with atoms.

Demystifying the Bohr Model in Relation to Neon

This exploration aims to demystify the Bohr Model, specifically as it relates to understanding neon's unique properties. We will dissect the model's core principles and apply them to neon's atomic structure to explain why it exhibits such distinctive behavior.

By the end of this discussion, we will hopefully shed light on how a relatively simple model, conceived over a century ago, can still provide valuable insights into the luminous mystery of neon. Our goal is to provide a clear picture of the relationship between atomic structure and observable phenomena.

The Bohr Model, therefore, offers us a simplified yet valuable framework for understanding neon's behavior. But before we can apply this model to our understanding of neon, it's crucial to first establish what exactly the Bohr Model entails and how it revolutionized our understanding of atomic structure.

Unveiling the Foundation: The Bohr Model Explained

The Bohr Model, a cornerstone of early 20th-century atomic theory, revolutionized our understanding of the atom. This model, while superseded by more sophisticated quantum mechanical models, provides a crucial stepping stone for comprehending the behavior of elements like neon.

Historical Context: A Revolution in Atomic Thought

Niels Bohr, a Danish physicist, introduced his model in 1913. His work built upon the discoveries of Max Planck and Albert Einstein regarding the quantization of energy, a concept that challenged classical physics. Bohr ingeniously applied these ideas to the structure of the atom, postulating that electrons could only exist in specific, discrete energy levels.

Before Bohr, Ernest Rutherford's model depicted the atom as a miniature solar system, with electrons orbiting a central nucleus.

However, Rutherford's model had a significant flaw: according to classical electromagnetism, orbiting electrons should continuously emit radiation, losing energy and spiraling into the nucleus. This implied that all atoms should be inherently unstable, which clearly contradicted reality.

Bohr's model ingeniously addressed this problem by quantizing the energy levels of electrons.

Core Principles of the Bohr Model

The Bohr Model rests on two fundamental principles that departed radically from classical physics:

Quantized Energy Levels

The first key postulate is that electrons can only occupy specific, quantized energy levels or orbits around the nucleus. These energy levels are often visualized as concentric shells, each corresponding to a distinct energy value. Electrons cannot exist between these levels; they are restricted to these specific orbits.

This concept of quantization was revolutionary. It explained why atoms were stable and did not continuously emit radiation. The energy levels are designated by the principal quantum number, n, where n = 1, 2, 3, and so on, corresponding to increasing energy levels further from the nucleus.

Electron Transitions

The second critical principle involves electron transitions between these energy levels. An electron can jump from one energy level to another by absorbing or emitting energy in the form of photons (light).

When an electron absorbs energy, it jumps to a higher energy level, a process called excitation. Conversely, when an electron drops to a lower energy level, it emits energy as a photon, a process called relaxation or emission.

The energy of the emitted or absorbed photon is precisely equal to the difference in energy between the two levels involved in the transition. This energy difference dictates the frequency (and therefore color) of the emitted light. This relationship is mathematically described by the equation: ΔE = hf, where ΔE is the energy difference, h is Planck's constant, and f is the frequency of the light.

The Bohr Model, therefore, offers us a simplified yet valuable framework for understanding neon's behavior. But before we can apply this model to our understanding of neon, it's crucial to first establish what exactly the Bohr Model entails and how it revolutionized our understanding of atomic structure.

Neon Through the Bohr Lens: Decoding the Element's Structure

Now that we have a firm grasp of the Bohr Model's core principles, we can finally turn our attention to neon itself. Applying the model to this specific element reveals insights into its unique characteristics and behavior, especially its remarkable inertness.

Neon: A Noble Resident of the Periodic Table

Neon (Ne) proudly resides in Group 18 of the periodic table, a group aptly named the noble gases. This designation is far from arbitrary. It signifies a family of elements renowned for their exceptional stability and reluctance to engage in chemical bonding.

The key to this nobility lies in their electron configurations, a concept perfectly illustrated by the Bohr Model.

The 2,8 Arrangement: A Recipe for Inertness

Neon boasts an electron configuration of 2,8. This means it has two electrons in its innermost shell (the K shell) and eight electrons in its outermost shell (the L shell).

The Bohr Model postulates that electrons fill the innermost shells first before occupying subsequent shells.

Significantly, the L shell can accommodate a maximum of eight electrons. Neon's L shell is thus completely filled, creating a particularly stable configuration.

This filled outer shell is the cornerstone of neon's inertness. It is this completed electron configuration that makes neon so stable and therefore disinclined to react with other elements.

Valence Electrons: The Guardians of Inertness

Valence electrons, those occupying the outermost shell, are the primary actors in chemical bonding.

Because Neon's outer shell is full, it already has eight valence electrons (an octet), so it has no "desire" or need to gain, lose, or share electrons to achieve stability.

This saturated valence shell means neon atoms have minimal tendency to interact with other atoms to form chemical bonds.

This is why neon exists as a monatomic gas under normal conditions. It prefers to remain aloof, a solitary entity, rather than participating in the molecular dances of other elements.

Now that we've established how the Bohr Model explains neon's stable electron configuration, it's time to explore the visual manifestation of these atomic properties: the light emitted by neon. This brings us to the fascinating world of atomic emission spectra and how neon's unique spectrum arises from the excitation and subsequent relaxation of its electrons.

The Light Show: Excitation, Emission, and Neon's Unique Spectrum

The vibrant glow of neon signs is perhaps the most recognizable application of this element. But the pretty colors are more than just aesthetics; they are a direct consequence of neon's atomic structure and the principles of quantum mechanics. Understanding how neon emits light requires delving into the concepts of atomic emission spectra, excitation, and relaxation.

Unveiling the Atomic Emission Spectrum

Every element possesses a unique fingerprint when it comes to light emission. This fingerprint is known as its atomic emission spectrum – a pattern of specific wavelengths of light that an element emits when excited.

Think of it as a barcode for atoms. Just as a barcode uniquely identifies a product, an atomic emission spectrum uniquely identifies an element.

Neon's emission spectrum, characterized by its bright orange-red glow, is distinct from those of other elements. This is due to the unique energy level spacing within neon atoms, a direct consequence of its electronic structure.

Excitation: Energizing Neon Atoms

For neon to emit light, its atoms must first be excited. Excitation refers to the process where an electron within the neon atom absorbs energy and jumps to a higher energy level.

In neon signs, this excitation is typically achieved by passing an electrical current through the gas. The electrical energy collides with neon atoms, transferring energy to their electrons.

Electrons don't stay in these higher energy levels forever. They are unstable, and the electron will be inclined to return to its original state.

Relaxation and Light Emission

Following excitation, the electron spontaneously "relaxes" or returns to a lower energy level. As it does so, it releases the excess energy in the form of a photon – a particle of light.

The energy of the emitted photon corresponds exactly to the energy difference between the higher and lower energy levels. Because energy levels within an atom are quantized (i.e., they have specific, discrete values), the emitted photons have specific energies, and therefore specific wavelengths.

These specific wavelengths create the characteristic lines observed in neon's atomic emission spectrum. It's this carefully tuned release of energy that allows us to witness the light show that is inherently neon.

The emission spectrum reveals a great deal about the allowed energy transitions within the neon atom. But to fully appreciate why neon exhibits this specific spectrum, and to understand the arrangement of its electrons within the atom, we need to introduce the concept of quantum numbers.

Quantum Numbers and Neon: Defining Shells and Energy

Quantum numbers are a set of numbers that describe the properties of an electron in an atom, including its energy level, shape of its orbital, and its orientation in space.

The most important of these, in the context of the Bohr model, is the principal quantum number, often denoted by the letter n.

The Principal Quantum Number (n): Energy Levels and Shells

The principal quantum number (n) directly correlates to the energy level of an electron and its distance from the nucleus. It can take on integer values: n = 1, 2, 3, and so on.

Higher values of n signify higher energy levels and greater average distances from the nucleus.

These energy levels are often referred to as electron shells, with n = 1 corresponding to the innermost shell (closest to the nucleus), also known as the K shell, n = 2 corresponding to the L shell, and so forth.

Neon's Electron Arrangement: K and L Shells

Now, let's apply this knowledge to neon.

Neon has 10 electrons in total. According to quantum mechanical principles, the n = 1 (K) shell can hold a maximum of 2 electrons.

Therefore, neon's two innermost electrons reside in the K shell.

The remaining 8 electrons then occupy the n = 2 (L) shell. This complete filling of the L shell is what confers neon its exceptional stability.

This configuration is often written as 1s²2s²2p⁶, however within the scope of Bohr's model we can simplify this to K(2), L(8).

Energy and Electron Excitation

The principal quantum number also helps to understand the energy required to excite an electron.

When a neon atom absorbs energy (e.g., from an electrical discharge), an electron can jump from a lower energy level (smaller n) to a higher energy level (larger n).

This requires a specific amount of energy that corresponds to the difference in energy between the two levels.

When the excited electron returns to its original lower energy level, it emits the excess energy as a photon of light.

The energy (and therefore the wavelength/color) of the emitted photon is directly related to the difference in energy levels dictated by the principal quantum number and the specific electron transition occurring.

Neon's two innermost electrons reside in the K shell, completely filling it. The remaining eight electrons then occupy the n = 2 (L) shell. This configuration of a filled outermost shell is what contributes to neon's stability and its reluctance to participate in chemical reactions. But while the Bohr model offers a simplified, intuitive picture of electron arrangement, it's essential to understand that it's not the complete story.

Beyond Bohr: Limitations and the Quantum Mechanical Model

The Bohr model, while a revolutionary step in understanding atomic structure, is not without its shortcomings. Its simplified depiction of electrons orbiting the nucleus in fixed paths, like planets around the sun, breaks down when applied to more complex atoms and phenomena. It's a stepping stone, not the final destination, in our understanding of the atomic world.

Inadequacies of the Bohr Model

One of the most significant limitations of the Bohr model is its inability to accurately predict and explain the spectra of atoms with more than one electron. While it works reasonably well for hydrogen, which has only one proton and one electron, the model struggles to account for the complex interactions between multiple electrons in larger atoms.

The model also fails to explain the fine details observed in atomic spectra, such as the splitting of spectral lines under the influence of magnetic fields (the Zeeman effect) or electric fields (the Stark effect). These phenomena require a more sophisticated model that considers the wave-like nature of electrons and the probabilistic distribution of their locations.

Furthermore, the Bohr model violates the Heisenberg uncertainty principle, which states that it is impossible to simultaneously know both the exact position and momentum of an electron. The Bohr model assumes that electrons have well-defined orbits, which directly contradicts this fundamental principle of quantum mechanics.

The Quantum Mechanical Leap: A More Complete Picture

To overcome these limitations, the quantum mechanical model was developed. This model treats electrons not as particles orbiting the nucleus in fixed paths, but as waves described by probability distributions called atomic orbitals.

These orbitals represent regions of space where an electron is most likely to be found.

The quantum mechanical model incorporates concepts such as electron spin, which influences the magnetic properties of atoms, and accounts for the complex interactions between electrons through mathematical equations that describe the behavior of these quantum systems.

Unlike the Bohr model's defined orbits, the quantum mechanical model provides a probabilistic description of electron location.

This allows it to explain phenomena that the Bohr model could not, such as the chemical bonding properties of molecules and the behavior of atoms in complex environments.

The mathematical framework is substantially more intricate, but the payoff is a much more accurate and comprehensive understanding of atomic structure and behavior. The quantum mechanical model doesn't negate the Bohr model entirely. It builds upon it, providing a more nuanced and accurate depiction of the atom. It shows how the Bohr model, despite its limitations, paved the way for further advancements in atomic theory.

Video: Neon's Atomic Secrets: Bohr Model Explained!

Play Video